Synergies in the space of control variables within the equilibrium-point hypothesis
- PMID: 26701299
- PMCID: PMC4716006
- DOI: 10.1016/j.neuroscience.2015.12.012
Synergies in the space of control variables within the equilibrium-point hypothesis
Abstract
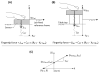
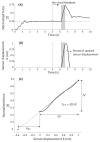
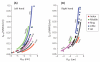
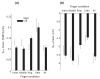
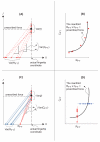
We use an approach rooted in the recent theory of synergies to analyze possible co-variation between two hypothetical control variables involved in finger force production based on the equilibrium-point (EP) hypothesis. These control variables are the referent coordinate (R) and apparent stiffness (C) of the finger. We tested a hypothesis that inter-trial co-variation in the {R; C} space during repeated, accurate force production trials stabilizes the fingertip force. This was expected to correspond to a relatively low amount of inter-trial variability affecting force and a high amount of variability keeping the force unchanged. We used the "inverse piano" apparatus to apply small and smooth positional perturbations to fingers during force production tasks. Across trials, R and C showed strong co-variation with the data points lying close to a hyperbolic curve. Hyperbolic regressions accounted for over 99% of the variance in the {R; C} space. Another analysis was conducted by randomizing the original {R; C} data sets and creating surrogate data sets that were then used to compute predicted force values. The surrogate sets always showed much higher force variance compared to the actual data, thus reinforcing the conclusion that finger force control was organized in the {R; C} space, as predicted by the EP hypothesis, and involved co-variation in that space stabilizing total force.
Keywords: apparent stiffness; equilibrium-point hypothesis; finger force; isometric; synergy; uncontrolled manifold hypothesis.
Copyright © 2015 IBRO. Published by Elsevier Ltd. All rights reserved.
Figures

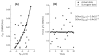


References
-
- Asatryan DG, Feldman AG. Functional tuning of the nervous system with control of movements or maintenance of a steady posture. I. Mechanographic analysis of the work of the limb on execution of a postural task. Biophysics. 1965;10:925–935.
-
- Bernstein N. The Coordination and Regulation of Movements. Pergamon Press; Oxford: 1967.
-
- Bizzi E, Giszter SF, Loeb E, Mussa-Ivaldi FA, Saltiel P. Modular organization of motor behavior in the frog's spinal cord. Trends Neurosci. 1995;18:442–446. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

