Object-oriented Persistent Homology
- PMID: 26705370
- PMCID: PMC4685963
- DOI: 10.1016/j.jcp.2015.10.036
Object-oriented Persistent Homology
Abstract
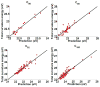
Persistent homology provides a new approach for the topological simplification of big data via measuring the life time of intrinsic topological features in a filtration process and has found its success in scientific and engineering applications. However, such a success is essentially limited to qualitative data classification and analysis. Indeed, persistent homology has rarely been employed for quantitative modeling and prediction. Additionally, the present persistent homology is a passive tool, rather than a proactive technique, for classification and analysis. In this work, we outline a general protocol to construct object-oriented persistent homology methods. By means of differential geometry theory of surfaces, we construct an objective functional, namely, a surface free energy defined on the data of interest. The minimization of the objective functional leads to a Laplace-Beltrami operator which generates a multiscale representation of the initial data and offers an objective oriented filtration process. The resulting differential geometry based object-oriented persistent homology is able to preserve desirable geometric features in the evolutionary filtration and enhances the corresponding topological persistence. The cubical complex based homology algorithm is employed in the present work to be compatible with the Cartesian representation of the Laplace-Beltrami flow. The proposed Laplace-Beltrami flow based persistent homology method is extensively validated. The consistence between Laplace-Beltrami flow based filtration and Euclidean distance based filtration is confirmed on the Vietoris-Rips complex for a large amount of numerical tests. The convergence and reliability of the present Laplace-Beltrami flow based cubical complex filtration approach are analyzed over various spatial and temporal mesh sizes. The Laplace-Beltrami flow based persistent homology approach is utilized to study the intrinsic topology of proteins and fullerene molecules. Based on a quantitative model which correlates the topological persistence of fullerene central cavity with the total curvature energy of the fullerene structure, the proposed method is used for the prediction of fullerene isomer stability. The efficiency and robustness of the present method are verified by more than 500 fullerene molecules. It is shown that the proposed persistent homology based quantitative model offers good predictions of total curvature energies for ten types of fullerene isomers. The present work offers the first example to design object-oriented persistent homology to enhance or preserve desirable features in the original data during the filtration process and then automatically detect or extract the corresponding topological traits from the data.
Keywords: Computational topology; Fullerene; Laplace-Beltrami flow; Protein; Total curvature energy; Variation.
Figures


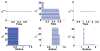









References
-
- Bates PW, Chen Z, Sun YH, Wei GW, Zhao S. Geometric and potential driving formation and evolution of biomolecular surfaces. J Math Biol. 2009;59:193–231. - PubMed
-
- Bates PW, Wei GW, Zhao S. The minimal molecular surface. Midwest Quantitative Biology Conference; Mission Point Resort, Mackinac Island, MI. September 29–October 1, 2006.
-
- Bates PW, Wei GW, Zhao Shan. Minimal molecular surfaces and their applications. Journal of Computational Chemistry. 2008;29(3):380–91. - PubMed
-
- Bendich Paul, Edelsbrunner Herbert, Kerber Michael. Computing robustness and persistence for images. IEEE Transactions on Visualization and Computer Graphics. 2010;16:1251–1260. - PubMed
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
