Regulatory mechanisms of group distributions in a gregarious arthropod

Abstract

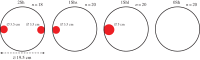
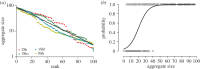
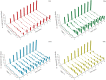
In a patchy environment, how social animals manage conspecific and environmental cues in their choice of habitat is a leading issue for understanding their spatial distribution and their exploitation of resources. Here, we experimentally tested the effects of environmental heterogeneities (artificial shelters) and some of their characteristics (size and fragmentation) on the aggregation process of a common species of terrestrial isopod (Crustacea). One hundred individuals were introduced into three different heterogeneous set-ups and in a homogeneous set-up. In the four set-ups, the populations split into two aggregates: one large (approx. 70 individuals) and one smaller (approx. 20 individuals). These aggregates were not randomly distributed in the arena but were formed diametrically opposite from one another. The similarity of the results among the four set-ups shows that under experimental conditions, the environmental heterogeneities have a low impact on the aggregation dynamics and spatial patterns of the isopod, merely serving to increase the probability of nucleation of the larger aggregation at these points. By contrast, the regulation of aggregate sizes and the regular distribution of groups are signatures of local amplification processes, in agreement with the short-range activator and long-range inhibitor model (scale-dependent feedbacks). In other words, we show how small-scale interactions may govern large-scale spatial patterns. This experimental illustration of spatial self-organization is an important step towards comprehension of the complex game of competition among groups in social species.

Keywords: aggregation; group size; local activation/long-range inhibition mechanism; patchy environment; scale-dependent feedbacks.

Figure 1.

Schematic of the four experimental set-ups.

Figure 2.

An example of aggregation dynamics in the arena with one shelter of ø 3.5 cm and 100 woodlice at t=5 min (a), t=10 min (b), t=30 min (c) and t=45 min (d), and its representation using Kernel density on the right side (paraboloid function). See other examples in the electronic supplementary material, figure S2.

Figure 3.

Mean dynamic of aggregation (number of woodlice as a function of time) in the first (a) and second (b) aggregate. Colours indicate the experimental condition.

Figure 4.

(a) Distribution of aggregate size (mean number of individuals included in the aggregate during its lifetime) during the experiments according to the set-up. Logarithmic scale for the y-axis. The solid line represents the mean exponential fitting of the pooled data Y =a.e^−bX with a=85.1 (±0.565) and b=−0.033 (±0.000319) (d.f.=270; R²=0.9876). (b) Probability that an aggregate will be present (=1) or dislocated (=0) at the 45th minute according to the maximum size (maximum number of aggregated individuals inside) reached during the experiment. The data are fitted by a logistic function y=a/(1+e^−c(x−T)) (R²=0.4616).

Figure 5.

(a) Angular distribution of the aggregates during the experiments. The value 0° is the normalized position of the first aggregate. The dotted line represents the mean fitting of the pooled data: y=a/(1+e^−c(x−T)) with a=0.689, T=124.187 and c=0.0205 (d.f.=8; R²=0.24). The first aggregate (0°) was excluded from the fitting. (b) Angular distribution of the aggregates presented at the end of experiments. 0° is the normalized position of the first aggregate. The solid line represents the mean fitting of the pooled data:=a/(1+e^−c(x−T)), with a=0.619, T=174.423 and c=0.0195 (d.f.=8; R²=0.48). The first aggregate (0°) was excluded from the fitting. (c) Size of all secondary aggregates (mean number of individuals during the aggregate lifetime) as a function of their angular position from the first aggregate (0°). Logarithmic scale for the y-axis. The solid line represents the mean fitting of the pooled data Y =2.45e^0.012X (d.f.=193; R²=0.23).

Figure 6.

Synthesis of the spatio-temporal distribution of aggregated individuals in the four set-ups. The value 0° is the normalized position of the principal aggregate.