Theory of oxygen transport to tissue
- PMID: 2673661
- PMCID: PMC5445261
Theory of oxygen transport to tissue
Abstract
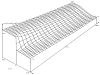
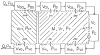
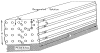
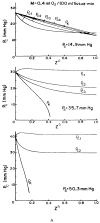
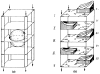
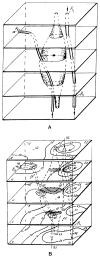
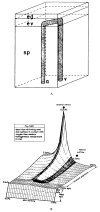
This review focuses on the theory of oxygen transport to tissue and presents the state of the art in mathematical modeling of transport phenomena. Results obtained with the classic Krogh tissue-cylinder model and recent advances in mathematical modeling of hemoglobin-oxygen kinetics, the role of hemoglobin and myoglobin in facilitating oxygen diffusion, and the role of morphologic and hemodynamic heterogeneities in oxygen transport in the microcirculation are critically discussed. Mathematical models simulate different parts of the pathway of oxygen molecules from the red blood cell, through the plasma, the endothelial cell, other elements of the vascular wall, and the extra- and intracellular space. Special attention in the review is devoted to intracapillary transport, which has been the subject of intensive theoretical research in the last decade. Models of pre- and postcapillary oxygen transport are also discussed. Applications to specific organs and tissues are reviewed, including skeletal muscle, myocardium, brain, lungs, arterial wall, and skin. Unresolved problems and major gaps in our knowledge of the mechanisms of oxygen transport are identified.
Figures
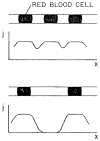
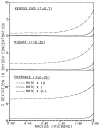
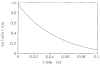
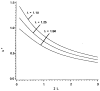




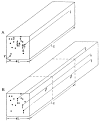
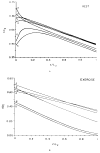
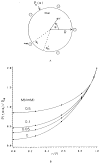
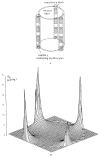


References
-
- Adair GS. The hemoglobin system. VI The oxygen dissociation curve of hemoglobin. J Biol Chem. 1925;63:529.
-
- Altman PL, Dittmer DS, editors. Respiration and Circulation. Federation of American Societies for Experimental Biology; Bethesda: 1971.
-
- Aroesty J, Gross JF. Convection and diffusion in the microcirculation. Microvasc Res. 1970;2:247. - PubMed
-
- Artigue RS, Hyman WA. The effect of myoglobin on the oxygen concentration in skeletal muscle subjected to ischemia. Ann Biomed Eng. 1976;4:128. - PubMed
-
- Artigue R, Bruley D, Von Rosenberg D, Mochizuki M. The effect of the red cell deoxigenation rate on oxygen delivery to tissue. Bibl Anat. 1977;15:405. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Molecular Biology Databases
