Inhibitory stabilization and visual coding in cortical circuits with multiple interneuron subtypes
- PMID: 26740531
- PMCID: PMC4808082
- DOI: 10.1152/jn.00732.2015
Inhibitory stabilization and visual coding in cortical circuits with multiple interneuron subtypes
Abstract
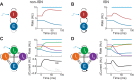
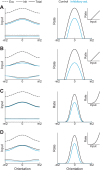
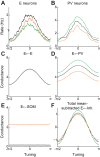
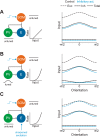
Recent anatomical and functional characterization of cortical inhibitory interneurons has highlighted the diverse computations supported by different subtypes of interneurons. However, most theoretical models of cortex do not feature multiple classes of interneurons and rather assume a single homogeneous population. We study the dynamics of recurrent excitatory-inhibitory model cortical networks with parvalbumin (PV)-, somatostatin (SOM)-, and vasointestinal peptide-expressing (VIP) interneurons, with connectivity properties motivated by experimental recordings from mouse primary visual cortex. Our theory describes conditions under which the activity of such networks is stable and how perturbations of distinct neuronal subtypes recruit changes in activity through recurrent synaptic projections. We apply these conclusions to study the roles of each interneuron subtype in disinhibition, surround suppression, and subtractive or divisive modulation of orientation tuning curves. Our calculations and simulations determine the architectural and stimulus tuning conditions under which cortical activity consistent with experiment is possible. They also lead to novel predictions concerning connectivity and network dynamics that can be tested via optogenetic manipulations. Our work demonstrates that recurrent inhibitory dynamics must be taken into account to fully understand many properties of cortical dynamics observed in experiments.
Keywords: V1; inhibition; modeling.
Copyright © 2016 the American Physiological Society.
Figures




References
-
- Avermann M, Tomm C, Mateo C, Gerstner W, Petersen CC. Microcircuits of excitatory and inhibitory neurons in layer 2/3 of mouse barrel cortex. J Neurophysiol 107: 3116–3134, 2012. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

