Mechanical Folding and Unfolding of Protein Barnase at the Single-Molecule Level

Abstract

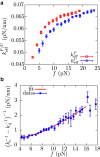
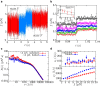
The unfolding and folding of protein barnase has been extensively investigated in bulk conditions under the effect of denaturant and temperature. These experiments provided information about structural and kinetic features of both the native and the unfolded states of the protein, and debates about the possible existence of an intermediate state in the folding pathway have arisen. Here, we investigate the folding/unfolding reaction of protein barnase under the action of mechanical force at the single-molecule level using optical tweezers. We measure unfolding and folding force-dependent kinetic rates from pulling and passive experiments, respectively, and using Kramers-based theories (e.g., Bell-Evans and Dudko-Hummer-Szabo models), we extract the position of the transition state and the height of the kinetic barrier mediating unfolding and folding transitions, finding good agreement with previous bulk measurements. Measurements of the force-dependent kinetic barrier using the continuous effective barrier analysis show that protein barnase verifies the Leffler-Hammond postulate under applied force and allow us to extract its free energy of folding, ΔG0. The estimated value of ΔG0 is in agreement with our predictions obtained using fluctuation relations and previous bulk studies. To address the possible existence of an intermediate state on the folding pathway, we measure the power spectrum of force fluctuations at high temporal resolution (50 kHz) when the protein is either folded or unfolded and, additionally, we study the folding transition-path time at different forces. The finite bandwidth of our experimental setup sets the lifetime of potential intermediate states upon barnase folding/unfolding in the submillisecond timescale.

Figure 1

Force-spectroscopy experiments with OT on barnase. (a) Not-to-scale scheme of the molecular experimental setup: barnase is linked to two dsDNA handles and the whole construct is inserted between two polystyrene beads. One bead is immobilized at the tip of a micropipette by air suction whereas the other is captured in the optical trap. Force is exerted to the captured bead and translated to the molecular system. (b) Example of FDC measured in pulling experiments performed at 60 nm/s. Under the stretching protocol (red), the molecule abruptly unfolds at ∼20 pN, whereas in the releasing protocol (blue), the molecule folds back at ∼4 pN (arrow). At ∼60 pN, we observe the overstretching transition of the handles. (Inset) Collection of stretching traces acquired in independent experiments, where it can be seen that unfolding forces f_U vary in each experiment. (c) Example of FTTs measured in passive experiments (i.e., at λ-constant). Each color is an independent experiment where barnase was initially set in state U at f_p = 3.6 pN. To see this figure in color, go online.

Figure 2

Elastic response of the peptide chain. (a) Effective stiffnesses along the folded and unfolded force branches, $k_{\text{eff}}^F$ (red open squares) and $k_{\text{eff}}^U$ (blue solid circles), respectively, obtained for one molecule. (b) Experimental measurement of ${\left({\left(k_{\text{eff}}^U\right)}^{-1}-{\left(k_{\text{eff}}^F\right)}^{-1}\right)}^{-1}$ and fit to Eq. 2 using the WLC elastic model (Eqs. S1 and S2). The resulting values for P and d_aa are given in Table 1. Data is obtained by averaging over 11 molecules. Error bars are standard statistical errors. To see this figure in color, go online.

Figure 3

Mechanical unfolding, folding, and TS of barnase. (a) Unfolding force histograms obtained at different pulling speeds. (b) Dependence of average unfolding forces 〈f_U〉 with loading rate r (r = $v{k}_{\text{eff}}^F$, where $k_{\text{eff}}^F$ ∼ 0.069 pN/nm). Fits to the analytical expressions provided by the BE (red line; Eq. S6) and DHS (green and blue lines for γ = 1/2 and 2/3, respectively; Eq. S8) models are shown. (c) Unfolding and folding kinetic rates, k_F→U(f) (gray, each symbol is associated to a different pulling speed in the range 25–960 nm/s) and k_F←U(f) (black), respectively, as a function of force. Fits to the analytical expressions provided by the BE and DHS models are shown (Eqs. S5 and S7, respectively). Color code as in (b). (d) Structure of barnase in the folded state. (Red) The first 25 amino acids to unfold in the mechanical unfolding process; (cyan) helices 2 and 3, which first unfold in chemical denaturation. (Blue) The hydrophobic core of the protein, dominated by β-sheets (made of a total of 29 amino acids); its formation corresponds to the TS-mediating mechanical folding from state U. (e) Two possible scenarios explain our experimental results for the mFEL of the protein barnase. (Left) There is a high-energy intermediate state surrounded by TS1, that is located close to state N and mediates unfolding at high forces, and TS2, that is located close to state U and mediates folding at low forces. (Right) The mFEL has a single TS that changes its position along the reaction coordinate as a function of force. To see this figure in color, go online.

Figure 4

Folding of barnase measured at high temporal resolution. (a) Example of FTTs recorded at a 50 kHz sampling rate that shows the folding of barnase as a sudden rise in force. (Red) Data for complete trajectory. (Blue) Data used for the alignment with other folding trajectories. (Boxed regions) Data used to compute the power spectrum of fluctuations when barnase is in state F (f_min = 3.8 pN, solid box) or U (f_max = 4.1 pN, dashed box). (b) Force-time trace obtained by aligning and averaging different folding trajectories (obtained at the same value of f_p) at the center of the force jump along a folding event and fits to a sigmoid function (Eq. 3). (Inset) The value τ_TP extracted from fit as a function of f_p, and relaxation time of the experimental setup (made by the bead in the optical trap, the handles, and the protein) as a function of force when barnase is at state F (solid line) or U (dashed line). (c) Power spectrum of the fluctuations of barnase recorded in passive mode experiments at 50 kHz for state F (blue circles) and U (red circles) at 4 pN. In each case, the fit to a double Lorentzian function (solid lines; Eq. S11) is shown, which allows us to determine the values of ν_f and ν_s, characteristic of the fast and slow relaxation modes. (d) Force-dependence of slow and fast frequency modes, ν_s and ν_f, respectively, obtained from the power spectrum of fluctuations measured in passive mode for the folded and unfolded states of barnase. To see this figure in color, go online.

Figure 5

Reconstruction of the kinetic barrier and free-energy recovery of barnase. (a) Profile of the kinetic barrier B(f) determined using the CEBA method. (Red squares are obtained from logk_F→U(f) (Eq. S14a), and blue squares are obtained from logk_F←U(f) (Eq. S14c).) By imposing the continuity of B(f) from extrapolation (gray-dashed curve), we estimate the free energy of formation of barnase, ΔG₀ = 20 ± 5 k_BT. Additionally, assuming that at large forces the kinetic barrier goes to zero, gives a lower bound for logk₀ ∼ 5 (hence, k₀ ∼ 150 s⁻¹). Error bars are computed using the bootstrap method and by propagation of the errors of the elastic parameters. (b) Stretching (red) and releasing (blue) work histograms, and results of the fit to Eq. S18 of the respective leftmost tails (black). Error bars are obtained using the bootstrap method. (Solid vertical lines) Free energy values obtained using the Jarzynski estimator with stretching and releasing work values independently. (Dashed vertical line) Free energy estimation obtained by correcting the effect of bias using the random energy model. (Inset) Convergence of the Jarzynski estimated corrected by the bias using the random energy model as a function with the number of work measurements n. To see this figure in color, go online.