A transcriptional signature of hub connectivity in the mouse connectome
- PMID: 26772314
- PMCID: PMC4747775
- DOI: 10.1073/pnas.1513302113
A transcriptional signature of hub connectivity in the mouse connectome
Abstract
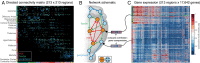
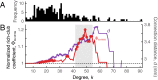
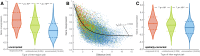
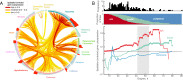
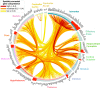
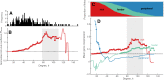
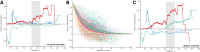
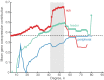
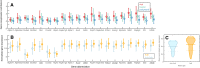
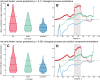
Connectivity is not distributed evenly throughout the brain. Instead, it is concentrated on a small number of highly connected neural elements that act as network hubs. Across different species and measurement scales, these hubs show dense interconnectivity, forming a core or "rich club" that integrates information across anatomically distributed neural systems. Here, we show that projections between connectivity hubs of the mouse brain are both central (i.e., they play an important role in neural communication) and costly (i.e., they extend over long anatomical distances) aspects of network organization that carry a distinctive genetic signature. Analyzing the neuronal connectivity of 213 brain regions and the transcriptional coupling, across 17,642 genes, between each pair of regions, we find that coupling is highest for pairs of connected hubs, intermediate for links between hubs and nonhubs, and lowest for connected pairs of nonhubs. The high transcriptional coupling associated with hub connectivity is driven by genes regulating the oxidative synthesis and metabolism of ATP--the primary energetic currency of neuronal communication. This genetic signature contrasts that identified for neuronal connectivity in general, which is driven by genes regulating neuronal, synaptic, and axonal structure and function. Our findings establish a direct link between molecular function and the large-scale topology of neuronal connectivity, showing that brain hubs display a tight coordination of gene expression, often over long anatomical distances, that is intimately related to the metabolic requirements of these highly active network elements.
Keywords: complex networks; connectome; hub; metabolism; rich club.
Conflict of interest statement
The authors declare no conflict of interest.
Figures



References
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources

