QUADRO: A SUPERVISED DIMENSION REDUCTION METHOD VIA RAYLEIGH QUOTIENT OPTIMIZATION

Abstract

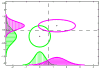
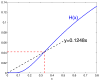
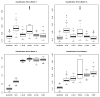
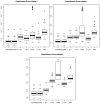
We propose a novel Rayleigh quotient based sparse quadratic dimension reduction method-named QUADRO (Quadratic Dimension Reduction via Rayleigh Optimization)-for analyzing high-dimensional data. Unlike in the linear setting where Rayleigh quotient optimization coincides with classification, these two problems are very different under nonlinear settings. In this paper, we clarify this difference and show that Rayleigh quotient optimization may be of independent scientific interests. One major challenge of Rayleigh quotient optimization is that the variance of quadratic statistics involves all fourth cross-moments of predictors, which are infeasible to compute for high-dimensional applications and may accumulate too many stochastic errors. This issue is resolved by considering a family of elliptical models. Moreover, for heavy-tail distributions, robust estimates of mean vectors and covariance matrices are employed to guarantee uniform convergence in estimating non-polynomially many parameters, even though only the fourth moments are assumed. Methodologically, QUADRO is based on elliptical models which allow us to formulate the Rayleigh quotient maximization as a convex optimization problem. Computationally, we propose an efficient linearized augmented Lagrangian method to solve the constrained optimization problem. Theoretically, we provide explicit rates of convergence in terms of Rayleigh quotient under both Gaussian and general elliptical models. Thorough numerical results on both synthetic and real datasets are also provided to back up our theoretical results.

Keywords: Classification; Rayleigh quotient; dimension reduction; oracle inequality; quadratic discriminant analysis.

Fig. 1

An example in ℝ². The green and purple represent class 1 and class 2, respectively. The ellipses are contours of distributions. Probability densities after being projected to X₁ and X₂ are also displayed. The dotted lines correspond to optimal thresholds for classification using each feature.

Fig. 2

Function $H(x)=\overline{\mathrm{\Phi }}(1/\sqrt{x})$.

Fig. 3

Distributions of minimum classification error based on 100 replications for four different normal models. The tuning parameters for QUADRO, SLR and L-SLR are chosen to minimize the classification errors of 4000 testing samples. See Fan et al. (2014) for detailed numerical tables.

Fig. 4

Distributions of minimum classification error based on 100 replications across different elliptical distribution models. The tuning parameters for QUADRO, SLR and L-SLR are chosen to minimize the classification errors. See Fan et al. (2014) for detailed numerical tables.

Fig. 5

Overall KEGG enrichment chart, using (a) QUADRO; (b) SLR.