Human brain networks function in connectome-specific harmonic waves

Abstract

A key characteristic of human brain activity is coherent, spatially distributed oscillations forming behaviour-dependent brain networks. However, a fundamental principle underlying these networks remains unknown. Here we report that functional networks of the human brain are predicted by harmonic patterns, ubiquitous throughout nature, steered by the anatomy of the human cerebral cortex, the human connectome. We introduce a new technique extending the Fourier basis to the human connectome. In this new frequency-specific representation of cortical activity, that we call 'connectome harmonics', oscillatory networks of the human brain at rest match harmonic wave patterns of certain frequencies. We demonstrate a neural mechanism behind the self-organization of connectome harmonics with a continuous neural field model of excitatory-inhibitory interactions on the connectome. Remarkably, the critical relation between the neural field patterns and the delicate excitation-inhibition balance fits the neurophysiological changes observed during the loss and recovery of consciousness.

Figure 1. Laplace eigenfunctions and connectome harmonics.

(a) Laplace eigenfunctions revealing the mechanical vibrations of rectangular metal plates (1st row)—first demonstrated by Ernst Chladni as patterns formed by sand on vibrating metal plates—and metal plates shaped as mammalian skin (2nd row) resembling different mammalian coat patterns for different frequency vibrations (images reprinted from with permission) as well as electron orbits of the hydrogen atom computed by time-independent Schrödinger's wave function (3rd row)—shown with increasing energy from left to right—and patterns emerging in electromagnetic interactions between laser-excited ion crystals (last row) (images adapted from15). (b) Workflow for the construction of macroscale connectome model. The graph representation was formed by connecting each node sampled from the cortical surface with its immediate local neighbours and by further including the long-range connections between the end points of the cortico-cortical and thalamo-cortical fibres. (c) Examples from the 20 lowest frequency connectome harmonics. Left: wave number. Right: spatial patterns of synchronous oscillations estimated by the eigenvectors of the connectome Laplacian.

Figure 2. Prediction of the RSNs by connectome harmonics.

(a) Patterns of synchronous oscillations, i.e., the RSNs, of the human brain overlap with the established functional systems, i.e., groups of cortical regions, which coactivate during certain tasks. For quantitative evaluation of any similarity between the RSNs and connectome harmonics, we use the seven RSNs (default mode, control, dorsal attention, ventral attention, visual, limbic and somato-motor networks) (shown in a) identified from 1,000 subjects' intrinsic functional connectivity data. (b) Similarity measured by mutual information and (c) predictive power measured by F-measure values between the connectome harmonics with 40 lowest frequencies and the reference RSNs in ref. (shown in a) compared with those of randomized harmonics (*P<0.0002, **P<0.0001 estimated by Monte Carlo simulations with 2,000 simulations per subject and 500,000 simulations for group average, after multiple comparison correction by false discovery rate, error bars indicate standard error across 10 subjects).

Figure 3. Reconstruction of the RSNs from connectome harmonic basis.

Normalized reconstruction error of each resting state network using (a) 0.1% and (b) 1.2% of the connectome harmonics spectrum averaged across 10 subjects (error bars and shading indicate standard error across 10 subjects) compared to the reconstruction of a randomized binary pattern. Red band in a highlights the steepest decrease for the DMN. (c) Reconstruction of the DMN using (from top to bottom) 5, 0.5 and 0.05% of the spectrum and the best matching connectome harmonic of one subject's data.

Figure 4. Neural field model.

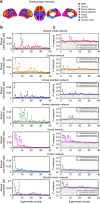
(a) Left: dynamics of excitatory (E) and inhibitory (I) activity. Right: time evolution of the excitatory E(v_i, t) and inhibitory I(v_i, t) activity at the cortical location at time t where , , and describe the diffusion processes of E and I activity acting on excitatory (EE, IE) and inhibitory (EI, II) neural populations and τ_s refers to the units of system time, that is, characteristic time scale. (b) Linear stability analysis of the neural field model in terms of connectome harmonics. The red regions correspond to the diffusion parameters in the phase space that algebraically satisfy the necessary condition for oscillations, that is, the critical Hopf regime, plotted as a function of the analysed diffusion parameter vertical axis and the eigenvalue of the connectome harmonic horizontal axis. (c) Power spectrum of the temporal oscillations in (a total of 267) numerical simulations averaged over all nodes. (d) Spatial pattern for an arbitrary time slice and the temporal profile of four seed locations shown in e. (f) Seed-based correlation analysis of the neural field patterns demonstrates the decoupling between the posterior and anterior midline nodes of the DMN for the same set of parameters leading to slow cortical oscillations.

Figure 5. Stability analysis of the neural field model.

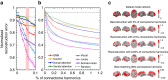
Stability of the emerging oscillations to external perturbation is tested by perturbing the neural field model for a sample oscillatory parameter set (, , and ). (a) The distance measure L(t) versus the time from perturbation t−t* where t* denotes the time of perturbation by white noise. Before the perturbation L(t) is identical to 0. L(0) shows how far the perturbed system altered from the underlying oscillatory stable state. After perturbation, that is, when t−t*>0, L(t) approaches 0 showing the system is Lyapunov stable. (b) The convergence of the limit cycle; that is, excitatory activity of two non-adjacent nodes plotted over time, of the perturbed (black solid line) to unperturbed (orange dashed line) system. (c) The original (unperturbed) trajectory (dashed line) and the perturbed trajectory (solid line) for two sample vertices (green and blue lines) after perturbation t−t*∈[0, 5] unit time. The perturbed trajectory converges back to the original trajectory (with a small phase shift) demonstrating that the state corresponding to the original trajectory is Lyapunov stable to small perturbations.