The temporal scaling of Caenorhabditis elegans ageing
- PMID: 26814965
- PMCID: PMC4828198
- DOI: 10.1038/nature16550
The temporal scaling of Caenorhabditis elegans ageing
Abstract
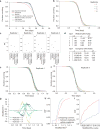
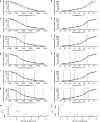
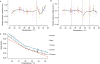
The process of ageing makes death increasingly likely, involving a random aspect that produces a wide distribution of lifespan even in homogeneous populations. The study of this stochastic behaviour may link molecular mechanisms to the ageing process that determines lifespan. Here, by collecting high-precision mortality statistics from large populations, we observe that interventions as diverse as changes in diet, temperature, exposure to oxidative stress, and disruption of genes including the heat shock factor hsf-1, the hypoxia-inducible factor hif-1, and the insulin/IGF-1 pathway components daf-2, age-1, and daf-16 all alter lifespan distributions by an apparent stretching or shrinking of time. To produce such temporal scaling, each intervention must alter to the same extent throughout adult life all physiological determinants of the risk of death. Organismic ageing in Caenorhabditis elegans therefore appears to involve aspects of physiology that respond in concert to a diverse set of interventions. In this way, temporal scaling identifies a novel state variable, r(t), that governs the risk of death and whose average decay dynamics involves a single effective rate constant of ageing, kr. Interventions that produce temporal scaling influence lifespan exclusively by altering kr. Such interventions, when applied transiently even in early adulthood, temporarily alter kr with an attendant transient increase or decrease in the rate of change in r and a permanent effect on remaining lifespan. The existence of an organismal ageing dynamics that is invariant across genetic and environmental contexts provides the basis for a new, quantitative framework for evaluating the manner and extent to which specific molecular processes contribute to the aspect of ageing that determines lifespan.
Figures




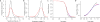



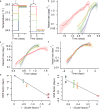
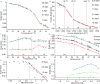
Comment in
-
Ageing: A stretch in time.Nature. 2016 Feb 4;530(7588):37-8. doi: 10.1038/nature16873. Epub 2016 Jan 20. Nature. 2016. PMID: 26814974 No abstract available.
References
-
- Herndon LA, et al. Stochastic and genetic factors influence tissue-specific decline in ageing C. elegans. Nature. 2002;419:808–814. - PubMed
-
- Shaw RF, Bercaw BL. Temperature and life-span in poikilothermous animals. Nature. 1962;196:454–457. - PubMed
-
- Mair W, Goymer P, Pletcher SD, Partridge L. Demography of dietary restriction and death in Drosophila. Science. 2003;301:1731–1733. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical
Miscellaneous

