Object Specific Trajectory Optimization for Industrial X-ray Computed Tomography

Abstract

In industrial settings, X-ray computed tomography scans are a common tool for inspection of objects. Often the object can not be imaged using standard circular or helical trajectories because of constraints in space or time. Compared to medical applications the variance in size and materials is much larger. Adapting the acquisition trajectory to the object is beneficial and sometimes inevitable. There are currently no sophisticated methods for this adoption. Typically the operator places the object according to his best knowledge. We propose a detectability index based optimization algorithm which determines the scan trajectory on the basis of a CAD-model of the object. The detectability index is computed solely from simulated projections for multiple user defined features. By adapting the features the algorithm is adapted to different imaging tasks. Performance of simulated and measured data was qualitatively and quantitatively assessed.The results illustrate that our algorithm not only allows more accurate detection of features, but also delivers images with high overall quality in comparison to standard trajectory reconstructions. This work enables to reduce the number of projections and in consequence scan time by introducing an optimization algorithm to compose an object specific trajectory.

Figure 1. Schematic of the system geometry.

The angles θ and ϕ describe the rotation of the object to be measured. One acquisition pose P_j is thus defined by an angle pair .

Figure 2. CAD models of the studied objects.

The region of interest (ROI) of the steel object is marked in red. Both renderings are in false colors.

Figure 3. Map of detectability index.

Top: the detectability index is drawn for all angle pairs (θ, ϕ), with white denoting a high value, and black a low value. Bottom: example simulated X-ray images are shown for three selected angle pairs: very good detectability with no overlaps (1), detectability affected by the metal tube (2), and overlaps of the ROI with the massive steel plate yielding very bad detectability (3).

Figure 4. Illustration of the trajectory optimization algorithm.

In each iteration the acquisition pose with the highest detectability index is selected. The right column shows the simulated measurement corresponding to the selected acquisition pose. The last row shows the final trajectory, consisting of 18 acquisition poses.

Figure 5. Reconstruction results of the steel object.

Reconstructions using the traditional circle trajectory (a,b) suffer from severe translucency problems. With the optimized trajectory the circular tube is reconstructed properly (c).

Figure 6. Results: Aluminium Cube Measured Data.

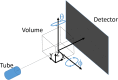
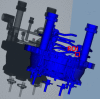
Comparison of reconstruction result of the aluminium cube from uniform sampling on a circle, with the optimized trajectory and the reference reconstruction from 1620 measured projections. The six feature points with the edges in X, Y and Z directions are enlarged.