Anatomically accurate high resolution modeling of human whole heart electromechanics: A strongly scalable algebraic multigrid solver method for nonlinear deformation
- PMID: 26819483
- PMCID: PMC4724941
- DOI: 10.1016/j.jcp.2015.10.045
Anatomically accurate high resolution modeling of human whole heart electromechanics: A strongly scalable algebraic multigrid solver method for nonlinear deformation
Abstract
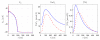
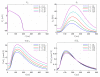
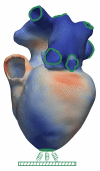
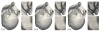
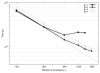
Electromechanical (EM) models of the heart have been used successfully to study fundamental mechanisms underlying a heart beat in health and disease. However, in all modeling studies reported so far numerous simplifications were made in terms of representing biophysical details of cellular function and its heterogeneity, gross anatomy and tissue microstructure, as well as the bidirectional coupling between electrophysiology (EP) and tissue distension. One limiting factor is the employed spatial discretization methods which are not sufficiently flexible to accommodate complex geometries or resolve heterogeneities, but, even more importantly, the limited efficiency of the prevailing solver techniques which are not sufficiently scalable to deal with the incurring increase in degrees of freedom (DOF) when modeling cardiac electromechanics at high spatio-temporal resolution. This study reports on the development of a novel methodology for solving the nonlinear equation of finite elasticity using human whole organ models of cardiac electromechanics, discretized at a high para-cellular resolution. Three patient-specific, anatomically accurate, whole heart EM models were reconstructed from magnetic resonance (MR) scans at resolutions of 220 μm, 440 μm and 880 μm, yielding meshes of approximately 184.6, 24.4 and 3.7 million tetrahedral elements and 95.9, 13.2 and 2.1 million displacement DOF, respectively. The same mesh was used for discretizing the governing equations of both electrophysiology (EP) and nonlinear elasticity. A novel algebraic multigrid (AMG) preconditioner for an iterative Krylov solver was developed to deal with the resulting computational load. The AMG preconditioner was designed under the primary objective of achieving favorable strong scaling characteristics for both setup and solution runtimes, as this is key for exploiting current high performance computing hardware. Benchmark results using the 220 μm, 440 μm and 880 μm meshes demonstrate efficient scaling up to 1024, 4096 and 8192 compute cores which allowed the simulation of a single heart beat in 44.3, 87.8 and 235.3 minutes, respectively. The efficiency of the method allows fast simulation cycles without compromising anatomical or biophysical detail.
Keywords: Algebraic Multigrid; Cardiac Electromechanics; Parallel Computing; Whole Heart Model.
Figures


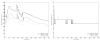



References
-
- Augustin CM. Classical and all-floating feti methods with applications to biomechanical models. Graz University of Technology; 2012. PhD thesis.
-
- Auricchio F, da Veiga LB, Lovadina C, Reali A, Taylor RL, Wriggers P. Approximation of incompressible large deformation elastic problems: some unresolved issues. Comput Mech. 2013;52(5):1153–1167.
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
