The prediction accuracy of dynamic mixed-effects models in clustered data

Abstract

Background: Clinical prediction models often fail to generalize in the context of clustered data, because most models fail to account for heterogeneity in outcome values and covariate effects across clusters. Furthermore, standard approaches for modeling clustered data, including generalized linear mixed-effects models, would not be expected to provide accurate predictions in novel clusters, because such predictions are typically based on the hypothetical mean cluster. We hypothesized that dynamic mixed-effects models, which incorporate data from previous predictions to refine the model for future predictions, would allow for cluster-specific predictions in novel clusters as the model is updated over time, thus improving overall model generalizability.

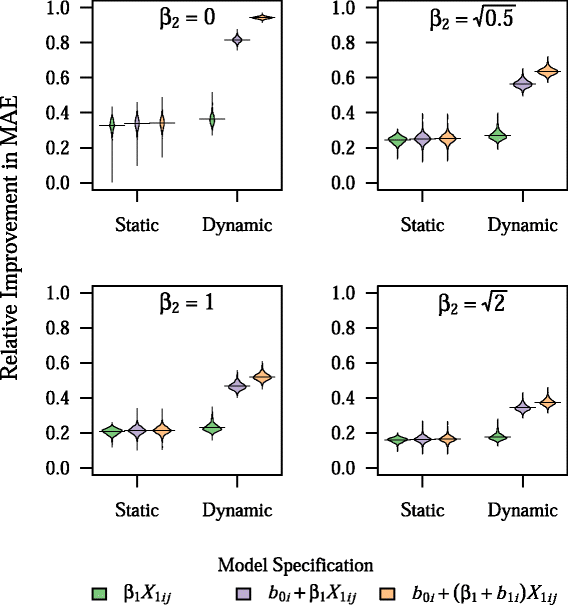
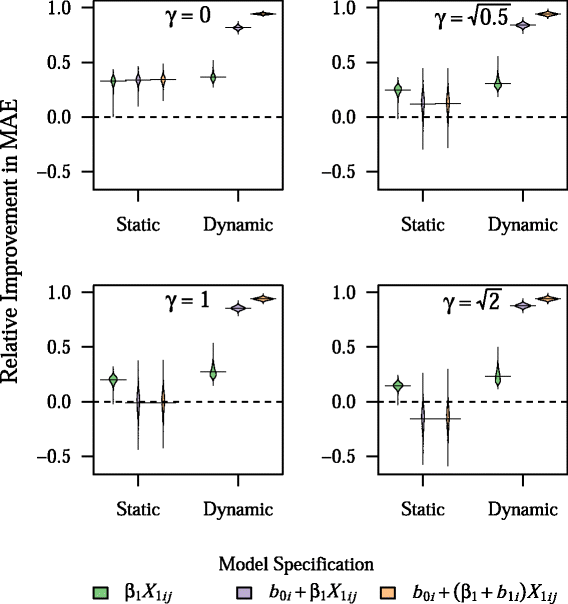
Results: We quantified the potential gains in prediction accuracy from using a dynamic modeling strategy in a simulation study. Furthermore, because clinical prediction models in the context of clustered data often involve outcomes that are dependent on patient volume, we examined whether using dynamic mixed-effects models would be robust to misspecification of the volume-outcome relationship. Our results indicated that dynamic mixed-effects models led to substantial improvements in prediction accuracy in clustered populations over a broad range of conditions, and were uniformly superior to static models. In addition, dynamic mixed-effects models were particularly robust to misspecification of the volume-outcome relationship and to variation in the frequency of model updating. The extent of the improvement in prediction accuracy that was observed with dynamic mixed-effects models depended on the relative impact of fixed and random effects on the outcome as well as the degree of misspecification of model fixed effects.

Conclusions: Dynamic mixed-effects models led to substantial improvements in prediction model accuracy across a broad range of simulated conditions. Therefore, dynamic mixed-effects models could be a useful alternative to standard static models for improving the generalizability of clinical prediction models in the setting of clustered data, and, thus, well worth the logistical challenges that may accompany their implementation in practice.

Keywords: Bayesian statistics; Clustered data; Dynamic modeling; Generalizability; Mixed-effects models; Prediction.

Fig. 1

Relative improvement in MAE for both dynamic and static models across all main parameter combinations. Plots show the density of values for relative improvement in MAE across 1,000 simulations, with horizontal bars representing the mean value. All other parameters are fixed at their base values. The center figure represents the base parameter combination

Fig. 2

Relative improvement in MAE by clinic-size quintile. Plots show the density of values for relative improvement in MAE across 1,000 simulations, with horizontal bars representing the mean value. These results are for the base parameter combination

Fig. 3

Effect of the update interval on the rate of improvement in prediction accuracy at a given clinic. This plot shows the mean relative improvement in MAE for prediction j at clinic i, across 1,000 simulations for different values of the update interval, θ. Vertical dashed and dotted lines indicate the point at which 80 % of the total gains in prediction accuracy have been achieved for the dynamic BLME model with a random intercept and the dynamic BLME model with a random intercept and random slope, respectively. Note that the base value of θ is 500, and all other parameters are fixed at their base values

Fig. 4

Effect of unknown patient-level predictor on model prediction accuracy. Plots show the density of values for relative improvement in MAE across 1,000 simulations, with horizontal bars representing the mean value, for different values of β ₂, which controls the size of the effect of the unknown patient-level predictor, X _2ij, to the outcome, Y _ij. Note that the relative contribution of X _2ij to the total variance in Y _ij, compared to X _1ij, is equal to β ₂². All other parameters are fixed at their base values

Fig. 5

Effect of an association between clinic size and the outcome on model prediction accuracy. Plots show the density of values for relative improvement in MAE across 1,000 simulations, with horizontal bars representing the mean value, for different values of γ, which controls the size of the effect of scaled clinic size, f(N _i), on the outcome, Y _ij. Note that the relative contribution of f(N _i) to the total variance in Y _ij, compared to X _1ij, is equal to γ ². All other parameters are fixed at their base values

Fig. 6

Effect of including clinic-size quintile as a fixed effect on prediction model accuracy. Plots show the density of values for relative improvement in MAE across 1,000 simulations, with horizontal bars representing the mean value, for different values of γ, which controls the size of the effect of scaled clinic size, f(N _i), on the outcome, Y _ij. All models include clinic-size quintile, N _i^*, as a categorical fixed effect, because N _i^* was defined to be observed while N _i was defined to be unobserved. Note that the relative contribution of f(N _i) to the total variance in Y _ij, compared to X _1ij, is equal to γ ². All other parameters are fixed at their base values

Fig. 7

Computational time of static and dynamic models. The mean computational times in seconds for the static models are shown by the open circles. From bottom to top, the circles represent the linear model, the BLME model with a random intercept, and the BLME model with a random intercept and a random slope. The mean computational times for the dynamic linear model, BLME model with a random intercept, and BLME model with a random intercept and a random slope, are shown by the solid, dashed, and dotted lines, respectively. All parameters are fixed at their base values