Pure-quartic solitons
- PMID: 26822758
- PMCID: PMC4740180
- DOI: 10.1038/ncomms10427
Pure-quartic solitons
Erratum in
-
Erratum: Pure-quartic solitons.Nat Commun. 2016 Mar 9;7:11048. doi: 10.1038/ncomms11048. Nat Commun. 2016. PMID: 26955800 Free PMC article. No abstract available.
Abstract
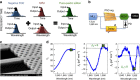
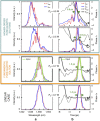
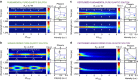
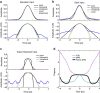
Temporal optical solitons have been the subject of intense research due to their intriguing physics and applications in ultrafast optics and supercontinuum generation. Conventional bright optical solitons result from the interaction of anomalous group-velocity dispersion and self-phase modulation. Here we experimentally demonstrate a class of bright soliton arising purely from the interaction of negative fourth-order dispersion and self-phase modulation, which can occur even for normal group-velocity dispersion. We provide experimental and numerical evidence of shape-preserving propagation and flat temporal phase for the fundamental pure-quartic soliton and periodically modulated propagation for the higher-order pure-quartic solitons. We derive the approximate shape of the fundamental pure-quartic soliton and discover that is surprisingly Gaussian, exhibiting excellent agreement with our experimental observations. Our discovery, enabled by precise dispersion engineering, could find applications in communications, frequency combs and ultrafast lasers.
Figures
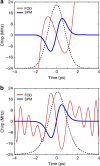
References
-
- Zabulsky N. J. & Kruskal M. D. Interactions of “solitons” in a collisionless plasma and the recurrence of initial states. Phys. Rev. Lett. 15, 240–243 (1965).
-
- Grelu P. & Akhmediev N. Dissipative solitons for mode-locked lasers. Nat. Photon. 6, 84–92 (2012).
-
- Herr T. et al. Temporal solitons in optical microresonators. Nat. Photon. 8, 145–152 (2014).
-
- Cundiff S. T. & Ye J. Colloquium: femtosecond optical frequency combs. Rev. Mod. Phys. 75, 325–342 (2003).
-
- Husakou A. V. & Herrmann J. Supercontinuum generation of higher-order solitons by fission in photonic crystal fibers. Phys. Rev. Lett. 87, 20390 (2001). - PubMed
Publication types
LinkOut - more resources
Full Text Sources
Other Literature Sources

