Emergence of core-peripheries in networks

Abstract

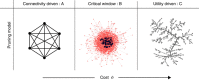
A number of important transport networks, such as the airline and trade networks of the world, exhibit a characteristic core-periphery structure, wherein a few nodes are highly interconnected and the rest of the network frays into a tree. Mechanisms underlying the emergence of core-peripheries, however, remain elusive. Here, we demonstrate that a simple pruning process based on removal of underutilized links and redistribution of loads can lead to the emergence of core-peripheries. Links are assumed beneficial if they either carry a sufficiently large load or are essential for global connectivity. This incentivized redistribution process is controlled by a single parameter, which balances connectivity and profit. The obtained networks exhibit a highly resilient and connected core with a frayed periphery. The balanced network shows a higher resilience than the world airline network or the world trade network, revealing a pathway towards robust structural features through pruning.

Figure 1. Schematic representation of the network classes obtained by our algorithm.

For vanishing cost, the network is fully connected (network A of six nodes—shown for simplicity) resembling the initial network. For significantly high cost, the network is tree-like, exhibiting no loops (network C of 10³ nodes). In between, the proposed pruning process generates a network (network B of 10³ nodes) with a core–periphery structure. The network in regime B was obtained for cost, θ=0.92, corresponding to a peak in the core–periphery measure (details in the text). For the central network, the layout was generated by applying the Fruchterman–Reingold algorithm. Colours show the difference in magnitude of coreness with black indicating the core and red, the periphery.

Figure 2. Average shortest path 〈d_ij〉 in km and average load 〈l_ij〉 dependence on cost θ.

We observe three different regimes as a function of the cost. In (a), the average shortest path length remains relatively stable while the load (a proxy for benefit) as shown in (b) increases drastically in regime B. The insets of both figures are blow-ups of regime B. In (a), a slight increase in the shortest path in regime B is observed, while in (b) the benefit increases by a large magnitude pointing to the inevitable compromise between connectivity and profit. Data are averages over 100 realizations.

Figure 3. Characteristic metrics of t-core decomposition.

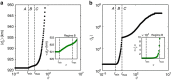
Core size, , and relative coreness, , versus the cost, θ. (a) A decay in the size of the core in regime B for increasing cost is shown. Core size increases again abruptly in the transition between regimes B and C as the pruning mechanism slows down. (b) Illuminates upon the comparison of the relative coreness of the core between a fully connected network in regime A and a core–periphery observed in regime B. The insets of both figures are blow-ups of regime B. The core of the network in regime B has a much lower coreness, which decays continuously with increasing cost until the network becomes a tree. Data are averages over 100 realizations.

Figure 4. Core–periphery measure λ as a function of θ for different system sizes N.

Modelled networks in regime B have a high value of λ owing to their core–periphery characteristic and resilience. The World Trade Network from year 1994 lies close to λ=0.041 and the World Airline Network from the year 2011 is at λ=0.0032. The trade network is only comprised of 80 nodes, whereas, the airline network has close to 3,500 nodes. Data are averages over 100 realizations.

Figure 5. Probability density functions of coreness of different regimes and the empirical WAN.

Regime B, for cost θ=0.92, that maximizes the value of core–periphery measure (independent of system size N), λ=0.248 (Fig. 4), and the real-world network exhibit a core–periphery structure. The density functions show the probability of having a shell with relative coreness (relative to a fully connected network). Data are averages over 100 realizations.

Figure 6. Modularity as a function of average degree.

The model networks show a peak* in the modularity for an average degree close to the World Airline Network. This peak is due to the increase in coreness of the network as the core collapses and a larger core takes shape (see Fig. 5—local peak** observed in the distribution of coreness for modelled networks). For the same average degree, L/N=5.6, the model generates many interconnected modules while the World Airline Network shows little or no links between modules. Different colours represent different communities and the size of the nodes classify them into core (large) or periphery (small). Data for system sizes N=200, 400 and 1,000 are averages over 100 realizations.