Evaluation of O2PLS in Omics data integration

Abstract

Background: Rapid computational and technological developments made large amounts of omics data available in different biological levels. It is becoming clear that simultaneous data analysis methods are needed for better interpretation and understanding of the underlying systems biology. Different methods have been proposed for this task, among them Partial Least Squares (PLS) related methods. To also deal with orthogonal variation, systematic variation in the data unrelated to one another, we consider the Two-way Orthogonal PLS (O2PLS): an integrative data analysis method which is capable of modeling systematic variation, while providing more parsimonious models aiding interpretation.

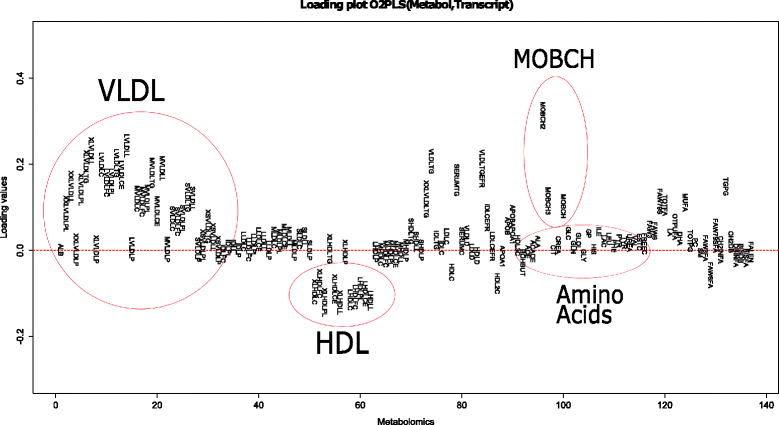
Results: A simulation study to assess the performance of O2PLS showed positive results in both low and higher dimensions. More noise (50 % of the data) only affected the systematic part estimates. A data analysis was conducted using data on metabolomics and transcriptomics from a large Finnish cohort (DILGOM). A previous sequential study, using the same data, showed significant correlations between the Lipo-Leukocyte (LL) module and lipoprotein metabolites. The O2PLS results were in agreement with these findings, identifying almost the same set of co-varying variables. Moreover, our integrative approach identified other associative genes and metabolites, while taking into account systematic variation in the data. Including orthogonal components enhanced overall fit, but the orthogonal variation was difficult to interpret.

Conclusions: Simulations showed that the O2PLS estimates were close to the true parameters in both low and higher dimensions. In the presence of more noise (50 %), the orthogonal part estimates could not distinguish well between joint and unique variation. The joint estimates were not systematically affected. Simultaneous analysis with O2PLS on metabolome and transcriptome data showed that the LL module, together with VLDL and HDL metabolites, were important for the metabolomic and transcriptomic relation. This is in agreement with an earlier study. In addition more gene expression and metabolites are identified being important for the joint covariation.

Fig. 1

Simulation: low dimensions little noise. Boxplots of 1000 simulations in which X (upper row) contains 500 samples and 100 variables, Y (lower row) contains 500 samples and 50 variables. Noise contributed for 5 % of the total variation. The first column corresponds to the joint part, the second column depicts the orthogonal part. The red line denotes the true loading profile

Fig. 2

Simulation: high dimensions little noise. Boxplots of 1000 simulations in which X (upper row) contains 500 samples and 500 variables, Y (lower row) contains 500 samples and 250 variables. Noise contributed for 5 % of the total variation. The first column corresponds to the joint part, the second column depicts the orthogonal part. The red line denotes the true loading profile

Fig. 3

Simulation: low dimensions high noise. Boxplots of 1000 simulations in which X contains 500 samples and 100 variables, Y contains 500 samples and 50 variables. Noise contributed for 50 % of the total variation. The first column corresponds to the joint part, the second column depicts the orthogonal part. The red line denotes the true loading profile

Fig. 4

Simulation: high dimensions high noise. Boxplots of 1000 simulations in which X contains 500 samples and 500 variables, Y contains 500 samples and 250 variables. Noise contributed for 50 % of the total variation. The first column corresponds to the joint part, the second column depicts the orthogonal part. The red line denotes the true loading profile

Fig. 5

Pearson correlation heatmap of metabolites. Red indicates high positive correlation, green is little correlation and blue is high negative correlation. The variables are in the original order. A histogram of correlations is added in the top left corner

Fig. 6

Scatterplot joint score vectors. The first joint score vectors (T, U) obtained from an O2PLS fit using Metabolomics (represented by T) and Transcriptomics (represented by U) are plotted against each other. The slope of the fitted line is 0.84, the intercept is zero due to the mean centering of the data. The coefficient of determination R ² was 0.47

Fig. 7

Labeled joint metabolomic loading plot. Four groups of interest are grouped: very-low-density-lipoproteins, high-density-lipoproteins, mobile lipids and amino acids

Fig. 8

O2PLS transcriptomic joint loadings. Joint part O2PLS loadings per gene expression. The top ten gene expressions are in black and green. The LL module gene expressions are in red and green. Four of the eleven gene expressions in the LL module are in the top ten, indicated in green. The loadings for five other gene expressions in the top ten and the loadings for the LL module gene expressions have opposite sign

Fig. 9

O2PLS metabolomic orthogonal loadings. Orthogonal part loadings obtained from an O2PLS fit with Metabolomics and Transcriptomics. One orthogonal component in metabolomics was identified

Fig. 10

O2PLS transcriptomic orthogonal loadings. Orthogonal part O2PLS loadings per gene expression. There were eight orthogonal components identified. The ratio of the first part sum of squares and last part sum of squares is approximately eleven