3off2: A network reconstruction algorithm based on 2-point and 3-point information statistics

Abstract

Background: The reconstruction of reliable graphical models from observational data is important in bioinformatics and other computational fields applying network reconstruction methods to large, yet finite datasets. The main network reconstruction approaches are either based on Bayesian scores, which enable the ranking of alternative Bayesian networks, or rely on the identification of structural independencies, which correspond to missing edges in the underlying network. Bayesian inference methods typically require heuristic search strategies, such as hill-climbing algorithms, to sample the super-exponential space of possible networks. By contrast, constraint-based methods, such as the PC and IC algorithms, are expected to run in polynomial time on sparse underlying graphs, provided that a correct list of conditional independencies is available. Yet, in practice, conditional independencies need to be ascertained from the available observational data, based on adjustable statistical significance levels, and are not robust to sampling noise from finite datasets.

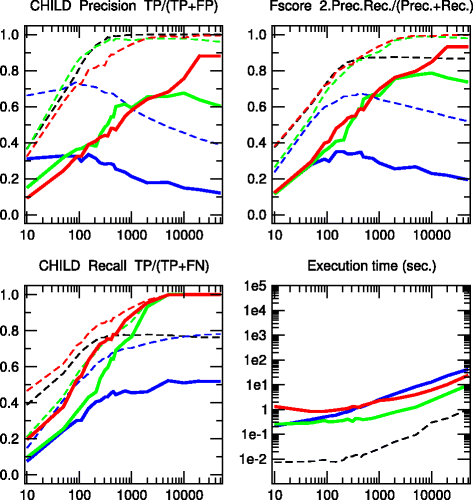
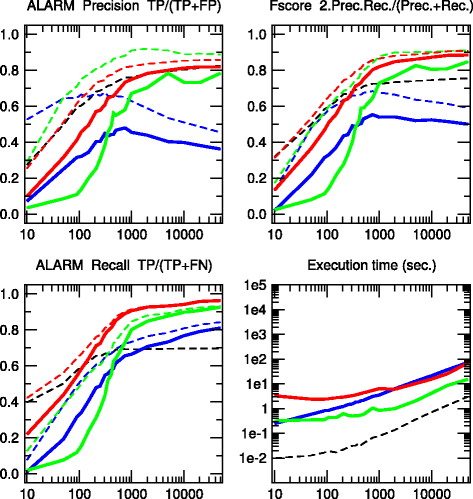
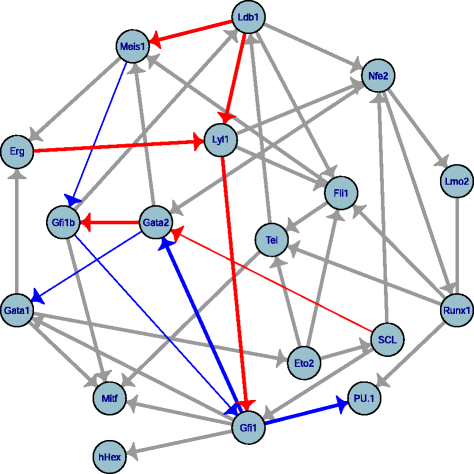
Results: We propose a more robust approach to reconstruct graphical models from finite datasets. It combines constraint-based and Bayesian approaches to infer structural independencies based on the ranking of their most likely contributing nodes. In a nutshell, this local optimization scheme and corresponding 3off2 algorithm iteratively "take off" the most likely conditional 3-point information from the 2-point (mutual) information between each pair of nodes. Conditional independencies are thus derived by progressively collecting the most significant indirect contributions to all pairwise mutual information. The resulting network skeleton is then partially directed by orienting and propagating edge directions, based on the sign and magnitude of the conditional 3-point information of unshielded triples. The approach is shown to outperform both constraint-based and Bayesian inference methods on a range of benchmark networks. The 3off2 approach is then applied to the reconstruction of the hematopoiesis regulation network based on recent single cell expression data and is found to retrieve more experimentally ascertained regulations between transcription factors than with other available methods.

Conclusions: The novel information-theoretic approach and corresponding 3off2 algorithm combine constraint-based and Bayesian inference methods to reliably reconstruct graphical models, despite inherent sampling noise in finite datasets. In particular, experimentally verified interactions as well as novel predicted regulations are established on the hematopoiesis regulatory networks based on single cell expression data.

Fig. 1

Inference of v-structures versus non-v-structures by 3-point information from observational data. a Isolated v-structures are predicted for I(x;y;z) < 0, and (b–d) isolated non-v-structures for I(x;y;z) > 0. e Generalized v-structures are predicted for I(x;y;z|{u _i}) < 0 and (f–h) generalized non-v-structures for I(x;y;z|{u _i}) > 0. In addition, as I(x;y;z|{u _i}) are invariant upon xyz permutations, the global orientation of v-structures and non-v-structures also requires to find the most likely base of the xyz triple. Choosing the base xy with the lowest conditional mutual information, i.e., I(x;y|{u _i})= minxyz(I(s;t|{u _i})), is found to be consistent with the Data Processing Inequality expected for (generalized) non-v-structures in the limit of infinite dataset, see main text. In practice, given a finite dataset, the inference of (generalized) v-structures versus non-v-structures can be obtained by replacing 3-point and 2-point information terms I(x;y|{u _i}) and I(x;y;z|{u _i}) by shifted equivalents, I ^′(x;y|{u _i}) and I ^′(x;y;z|{u _i}), including finite size corrections, see text (Eqs. 23 & 24)

Fig. 2

CHILD network. [20 nodes, 25 links, 230 parameters, Average degree 2.5, Maximum in-degree 2]. Precision, Recall and F-score for skeletons (dashed lines) and CPDAGs (solid lines). The results are given for Aracne (black), PC (blue), Bayesian Hill-Climbing (green) and 3off2 (red)

Fig. 3

ALARM network. [37 nodes, 46 links, 509 parameters, Average degree 2.49, Maximum in-degree 4]. Precision, Recall and F-score for skeletons (dashed lines) and CPDAGs (solid lines). The results are given for Aracne (black), PC (blue), Bayesian Hill-Climbing (green) and 3off2 (red)

Fig. 4

INSURANCE network. [27 nodes, 52 links, 984 parameters, Average degree 3.85, Maximum in-degree 3]. Precision, Recall and F-score for skeletons (dashed lines) and CPDAGs (solid lines). The results are given for Aracne (black), PC (blue), Bayesian Hill-Climbing (green) and 3off2 (red)

Fig. 5

BARLEY network. [48 nodes, 84 links, 114,005 parameters, Average degree 3.5, Maximum in-degree 4]. Precision, Recall and F-score for skeletons (dashed lines) and CPDAGs (solidlines). The results are given for Aracne (black), PC (blue), Bayesian Hill-Climbing (green) and 3off2 (red)

Fig. 6

HEPAR II network. [70 nodes, 123 links, 1,453 parameters, Average degree 3.51, Maximum in-degree 6]. Precision, Recall and F-score for skeletons (dashed lines) and CPDAGs (solid lines). The results are given for Aracne (black), PC (blue), Bayesian Hill-Climbing (green) and 3off2 (red)

Fig. 7

Hematopoietic subnetwork reconstructed by 3off2. The dataset [36] concerns 18 transcription factors, 597 single cells, 5 different hematopoietic progenitor types. Red and blue edges correspond to experimentally proven activations and repressions, respectively as reported in the literature (Table 1), while grey links indicate regulatory interactions for which no clear evidence has been established so far. Thinner arrows underline 3off2 misorientations