Robust bidirectional links for photonic quantum networks
- PMID: 26824069
- PMCID: PMC4730861
- DOI: 10.1126/sciadv.1500672
Robust bidirectional links for photonic quantum networks
Abstract
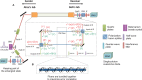
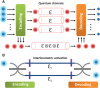
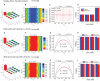
Optical fibers are widely used as one of the main tools for transmitting not only classical but also quantum information. We propose and report an experimental realization of a promising method for creating robust bidirectional quantum communication links through paired optical polarization-maintaining fibers. Many limitations of existing protocols can be avoided with the proposed method. In particular, the path and polarization degrees of freedom are combined to deterministically create a photonic decoherence-free subspace without the need for any ancillary photon. This method is input state-independent, robust against dephasing noise, postselection-free, and applicable bidirectionally. To rigorously quantify the amount of quantum information transferred, the optical fibers are analyzed with the tools developed in quantum communication theory. These results not only suggest a practical means for protecting quantum information sent through optical quantum networks but also potentially provide a new physical platform for enriching the structure of the quantum communication theory.
Keywords: Bidirectional quantum communication; decoherence-free subspace; polarization-maintaining fiber; quantum capacity.
Figures
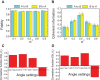
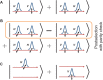
Similar articles
-
Two-photon quantum walk in a multimode fiber.Sci Adv. 2016 Jan 29;2(1):e1501054. doi: 10.1126/sciadv.1501054. eCollection 2016 Jan. Sci Adv. 2016. PMID: 27152325 Free PMC article.
-
Ultrafast optical control of individual quantum dot spin qubits.Rep Prog Phys. 2013 Sep;76(9):092501. doi: 10.1088/0034-4885/76/9/092501. Epub 2013 Sep 4. Rep Prog Phys. 2013. PMID: 24006335 Review.
-
Local conversion of four Einstein-Podolsky-Rosen photon pairs into four-photon polarization-entangled decoherence-free states with non-photon-number-resolving detectors.Opt Express. 2011 Dec 5;19(25):25433-40. doi: 10.1364/OE.19.025433. Opt Express. 2011. PMID: 22273935
-
A single-crystal source of path-polarization entangled photons at non-degenerate wavelengths.Opt Express. 2008 Jun 23;16(13):9701-7. doi: 10.1364/oe.16.009701. Opt Express. 2008. PMID: 18575538
-
Photonic quantum information: science and technology.Proc Jpn Acad Ser B Phys Biol Sci. 2016;92(1):29-43. doi: 10.2183/pjab.92.29. Proc Jpn Acad Ser B Phys Biol Sci. 2016. PMID: 26755398 Free PMC article. Review.
Cited by
-
Avoiding disentanglement of multipartite entangled optical beams with a correlated noisy channel.Sci Rep. 2017 Mar 15;7:44475. doi: 10.1038/srep44475. Sci Rep. 2017. PMID: 28295024 Free PMC article.
-
Universal bound on sampling bosons in linear optics and its computational implications.Natl Sci Rev. 2019 Jul;6(4):719-729. doi: 10.1093/nsr/nwz048. Epub 2019 Apr 9. Natl Sci Rev. 2019. PMID: 34691927 Free PMC article.
-
Decoherence Control of Nitrogen-Vacancy Centers.Sci Rep. 2017 Sep 20;7(1):11937. doi: 10.1038/s41598-017-12280-z. Sci Rep. 2017. PMID: 28931932 Free PMC article.
-
Chip-Based High-Dimensional Optical Neural Network.Nanomicro Lett. 2022 Nov 14;14(1):221. doi: 10.1007/s40820-022-00957-8. Nanomicro Lett. 2022. PMID: 36374430 Free PMC article.
-
Deterministic quantum teleportation through fiber channels.Sci Adv. 2018 Oct 19;4(10):eaas9401. doi: 10.1126/sciadv.aas9401. eCollection 2018 Oct. Sci Adv. 2018. PMID: 30345350 Free PMC article.
References
-
- Kok P., Munro W. J., Nemoto K., Ralph T. C., Dowling J. P., Milburn G. J., Linear optical quantum computing with photonic qubits. Rev. Mod. Phys. 79, 135–174 (2007).
-
- Aspuru-Guzik A., Walther P., Photonic quantum simulators. Nat. Phys. 8, 285–291 (2012).
-
- Giovannetti V., Lloyd S., Maccone L., Advances in quantum metrology. Nat. Photonics 5, 222–229 (2011).
-
- Kao K. C., Hockham G. A., Dielectric-fibre surface waveguides for optical frequencies. Proc. IEE 113, 1151–1158 (1966).
-
- A. Kumar, A. Ghatak, Polarization of Light with Applications in Optical Fibers (SPIE Press, Bellingham, WA, 2011).
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
Molecular Biology Databases

