Evolution of genetic instability in heterogeneous tumors

Abstract

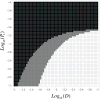
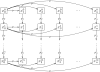
Genetic instability is an important characteristic of cancer. While most cancers develop genetic instability at some stage of their progression, sometimes a temporary rise of instability is followed by the return to a relatively stable genome. Neither the reasons for these dynamics, nor, more generally, the role of instability in tumor progression, are well understood. In this paper we develop a class of mathematical models to study the evolutionary competition dynamics among different sub-populations in a heterogeneous tumor. We observe that despite the complexity of this multi-component and multi-process system, there is only a small number of scenarios expected in the context of the evolution of instability. If the penalty incurred by unstable cells (the decrease in the growth due to deleterious mutations) is high compared with the gain (the production rate of advantageous mutations), then instability does not evolve. In the opposite case, instability evolves and comes to dominate the system. In the intermediate parameter regime, instability is generated but later gives way to stable clones. Moreover, the model also informs us of the patterns of instability for cancer lineages corresponding to different stages of progression. It is predicted that mutations causing instability are merely "passengers" in tumors that have undergone only a small number of malignant mutations. Further down the path of carcinogenesis, however, unstable cells are more likely to give rise to the winning clonal wave that takes over the tumor and carries the evolution forward, thus conferring a causal role of the instability in such cases. Further, each individual clonal wave (i.e. cells harboring a fixed number of malignant driver mutations) experiences its own evolutionary history. It can fall under one of three types of temporal behavior: stable throughout, unstable to stable, or unstable throughout. Which scenario is realized depends on the subtle (but predictable) interplay among mutation rates and the death toll associated with the instability. The modeling approach provided here sheds light onto important aspects of the evolutionary dynamics of instability, which may be relevant to treatment scenarios that target instability or damage repair.

Keywords: Chromosomal instability; Driver mutation; Microsatellite instability; Passenger mutation.

Figure 1. Diagram for two simple models

Variables x_i, 0 ≤ i ≤ n represent non-cancerous populations and y_i, 0 ≤ i ≤ n represent the cancer populations. The index indicates the level of instability. Parameters d_i represent death rates of populations x_i and y_i, parameters p_i represent instability induced mutation rates, μ, μ_i, 0 ≤ i ≤ n and ν_i, 0, ≤ i ≤ n represent mutations generating the unstable types. (a) Radial mutation network model. (b) Sequential mutation network model.

Figure 2. Plots of cancerous and non-cancerous populations for radial mutation network, equations (3–6)

(a) The populations x_i, log₁₀D = −1.2. Non-cancerous populations stay relatively stable for all values of t. (b) Cancerous population for an intermediate death rate, log₁₀D = −1.2. In this case the more unstable populations are larger at the beginning of growth, but as tumor progress the system switches to higher number of cells in more stable populations. The rest of parameters are d₀ = 10⁻⁴, p₀ = 10⁻⁷, p₁ = 10⁻⁴, a = 1.2, μ = 10⁻⁷, n = 3.

Figure 3. The dynamics of the instability index for models with one driver mutation and many driver mutation

➀, ➁, ➂ correspond to the three cases in section 3.1. (a) One driver mutation model with quasispecies equations, radial mutation network: n = 3, a = 1.2, μ = 10⁻⁷, p₀ = 10⁻⁷, p₁ = 10⁻⁵, p₂ = 10^−3.5, p₃ = 10⁻², d₀ = 10⁻⁴, d₁ = 10⁻³, 10^−2.5, 10^−3.5, d₂ = 10^−1.5, 10⁻², 10⁻³, d₃ = 10^−0.5, 10^−2.5 for cases ➀, ➁, ➂ respectively. (b) Many driver mutation model with logistic growth equations, radial mutation network: n = 3, m = 6, $K_{x_i^0}={10}^5$, $K_{x_i^1}=K_{x_i^2}={10}^7$, $K_{x_i^3}=K_{x_i^4}={10}^{12}$, $K_{x_i^5}=K_{x_i^6}={10}^{15}$, a_i = 1 + 0.05i, 0 ≤ i ≤ 6, μ = 10⁻⁷, p₀ = 10⁻⁷, p₁ = 10⁻⁵, p₂ = 10⁻³, p₃= 10⁻², d₀ = 10⁻⁴, d₁ = 10^−0.5, 10⁻¹, d₂ = 10^−0.2, 10^−0.3, 10^−0.5, d₃ =10^−0.1, 10^−0.15, 10^−0.2, for cases ➀, ➁, ➂ respectively.

Figure 4. Level of instability depending on the parameters D and p₁ for radial mutation network model

Black corresponds to low levels of instability at all times, white to high level of instability at all times, and gray to high level of instability at first then switching to stability. The parameters are d₀ = 10⁻⁴, p₀ = 10⁻⁷, a = 1.2, μ = 10⁻⁷, n = 1.

Figure 5. Three scenarios for different dynamic versions of the radial mutation network model

(a) Quasispecies-type equations with partial homeostatic control for y, (b) Quasispecies-type equations without homeostatic control for y. (c) Logistic growth equations. For all these models it is possible to get all three scenarios by only changing the magnitude of the death rates D. In (b) and (c) the cancer population reaches its maximum value faster. The parameters d₀ = 10⁻⁴, p₀ = 10⁻⁷, p₁ = 10⁻⁴, a = 1.2, μ = 10⁻⁷, n = 4.

Figure 6. The level of instability depending on the number of unstable types, n for radial mutation network

Displayed are plots for n = 2, 5, 10, 50. Higher numbers of populations correspond to more instability in the system. The parameters are log₁₀ D = −0.7, d₀ = 10⁻⁴, p₀ = 10⁻⁷, a = 1.2, n = 4, μ_i = p_i for i ≥ 1.

Figure 7

Radial mutation network involving multiple driver mutations.

Figure 8. Temporal dynamics of different sub-populations with multiple driver mutations

Radial mutation network with logistic growth equations. Each plot corresponds to a single step in carcinogenesis and plots the subpopulations at different instability levels. m = 3, n = 3, d₀ = 10⁻⁴, d₁ = 10⁻⁴, d₀ = 10⁻³, d₂ = 10⁻², d₃ = 10⁻¹, p₀ = 10⁻⁷, p₁ = 10⁻⁵, p₂ = 10^−3.5, p₃ = 10⁻², $K_{x_i^0}={10}^5$, $K_{x_i^1}={10}^7$, $K_{x_i^2}={10}^{12}$, $K_{x_i^3}={10}^{15}$, a₀ = 1, a₁ = 1.05, a₂ = 1.1, a₃ = 1.15, a₄ = 1.2.

Figure 9. The dynamics of the instability in the presence of back mutations

(a) Radial mutation network with multiple driver mutations. ➀, ➁, ➂ correspond to the three cases in section 3.1. n = 3, m = 6, $K_{x_i^0}={10}^5$, $K_{x_i^1}=K_{x_i^2}={10}^7$, $K_{x_i^3}=K_{x_i^4}={10}^{12}$, $K_{x_i^5}=K_{x_i^6}={10}^{15}$, a_i = 1 + 0.05i, 0 ≤ i ≤ 6, μ = 10⁻⁷, p₀ = 10⁻⁷, p₁ = 10⁻⁵, p₂ = 10⁻³, p₃ = 10⁻², d₀ = 10⁻⁴, d₁ = 10^−0.5, 10⁻¹, 10⁻², d₂ = 10^−0.3, 10^−0.4, 10⁻¹, d₃ = 10^−0.1, 10^−0.27, 10^−0.2, for cases ➀, ➁, ➂ respectively. (b) Level of instability depending on the parameters D and p₁ for radial mutation network model with a single driver mutation. Black corresponds to low levels of instability at all times, white to high level of instability at all times, and gray to high level of instability at first then switching to stability. The parameters are d₀ = 10⁻⁴, p₀ = 10⁻⁷, a = 1.2, μ = 10⁻⁷, n = 1.