A micro-scale simulation of red blood cell passage through symmetric and asymmetric bifurcated vessels

Abstract

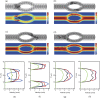
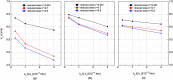
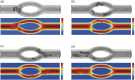
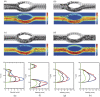
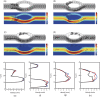
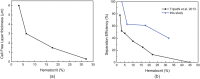
Blood exhibits a heterogeneous nature of hematocrit, velocity, and effective viscosity in microcapillaries. Microvascular bifurcations have a significant influence on the distribution of the blood cells and blood flow behavior. This paper presents a simulation study performed on the two-dimensional motions and deformation of multiple red blood cells in microvessels with diverging and converging bifurcations. Fluid dynamics and membrane mechanics were incorporated. Effects of cell shape, hematocrit, and deformability of the cell membrane on rheological behavior of the red blood cells and the hemodynamics have been investigated. It was shown that the blood entering the daughter branch with a higher flow rate tended to receive disproportionally more cells. The results also demonstrate that red blood cells in microvessels experienced lateral migration in the parent channel and blunted velocity profiles in both straight section and daughter branches, and this effect was influenced by the shape and the initial position of the cells, the hematocrit, and the membrane deformability. In addition, a cell free region around the tip of the confluence was observed. The simulation results are qualitatively consistent with existing experimental findings. This study may provide fundamental knowledge for a better understanding of hemodynamic behavior of micro-scale blood flow.

Figure 1

(a) Schematic model of a microvessel with diverging and converging bifurcations. (b) From left to right: red blood cell shapes obtained for reduced area s^* = 0.481, 0.7 and 0.9.

Figure 2

Motion of a file of 8 red blood cells (Hct = 3.2%) in the symmetric bifurcated microchannel at time instants (a) t = 0.71 ms, (b) t = 1.43 ms, (c) t = 1.91 ms, and (d) t = 5.00 ms. Velocity vectors (upper panels) and axial velocity magnitude contours (cm/s) (lower panels) are presented. The reduced area s^* = 0.481. The spring constant of the cell membrane was k_l = k_b = 3.0 × 10⁻¹³ Nm. Velocity profiles at different locations of the microvessel for different hematocrits: (e) at the apex of the diverging bifurcation at t = 0.75 ms, (f) at the mid cross section of the bifurcation at t = 1.50 ms, (g) at the apex of the converging bifurcation at t = 2.00 ms, and (h) at the cross section 2 μm from the right outlet at t = 5.00 ms. Blue line: 8 red blood cells (Hct = 3.2%); red line: 16 red blood cells (Hct = 6.4%); black line: 44 red blood cells (Hct = 17.6%); green line: 80 red blood cells (Hct = 32%).

Figure 3

Motion of a file of 8 red blood cells (Hct = 3.2%) in the symmetric bifurcated microchannel at time instants (a) t = 0.55 ms, (b) t = 1.16 ms, (c) t = 1.66 ms, and (d) t = 5.00 ms. Velocity vectors (upper panels) and axial velocity magnitude contours (cm/s) (lower panels) are presented. The reduced area s^* = 0.481. The spring constant of the cell membrane was k_l = k_b = 3.0 × 10⁻¹² Nm.

Figure 4

Motion of a file of 8 red blood cells (Hct = 3.2%) in the symmetric bifurcated microchannel at time instants (a) t = 0.74 ms, (b) t = 1.44 ms, (c) t = 1.93 ms, and (d) t = 5.00 ms. Velocity vectors (upper panels) and axial velocity magnitude contours (cm/s) (lower panels) are presented. The reduced area s^* = 0.7. The spring constant of the cell membrane was k_l = k_b = 3.0 × 10⁻¹³ Nm.

Figure 5. Dependence of transit velocity of erythrocytes in the symmetric bifurcated microchannel on cell membrane stiffness.

(a) The initial distance between cell center and the axis of the channel h_off = 0 μm (coaxial). (b) h_off = 2.5 μm (noncoaxial). (c) h_off = 5 μm (noncoaxial).

Figure 6

Motion of a file of 8 red blood cells (Hct = 3.2%) in the asymmetric bifurcated microchannel at time instants (a) t = 0.75 ms, (b) t = 1.54 ms, (c) t = 2.40 ms, and (d) t = 5.00 ms. Velocity vectors (upper panels) and axial velocity magnitude contours (cm/s) (lower panels) are presented. The reduced area s^* = 0.481. The spring constant of the cell membrane was k_l = k_b = 3.0 × 10⁻¹³ Nm. Velocity profiles at different locations of the microvessel for different initial cell positions: (e) at the apex of the diverging bifurcation at t = 0.75 ms, (f) at the mid cross section of the bifurcation at t = 1.50 ms, (g) at the apex of the converging bifurcation at t = 2.40 ms, and (h) at the cross section 2 μm from the right outlet at t = 5.00 ms. Blue line: h_off = 0 μm (coaxial) initially; red line: h_off = 2.5 μm (noncoaxial) initially; black line: h_off = 5 μm (noncoaxial) initially.

Figure 7

Motion of two files of 44 red blood cells (Hct = 17.6%) in the asymmetric bifurcated microchannel at time instants (a) t = 1.20 ms, (b) t = 1.80 ms, (c) t = 2.40 ms, and (d) t = 5.00 ms. Velocity vectors (upper panels) and axial velocity magnitude contours (cm/s) (lower panels) are presented. The reduced area s^* = 0.481. The spring constant of the cell membrane was k_l = k_b = 3.0 × 10⁻¹³ Nm. Velocity profiles at different locations of the microvessel for different hematocrits: (e) at the apex of the diverging bifurcation at t = 1.20 ms, (f) at the mid cross section of the bifurcation at t = 1.80 ms, (g) at the apex of the converging bifurcation at t = 2.40 ms, and (h) at the cross section 2 μm from the right outlet at t = 5.00 ms. Blue line: 8 red blood cells (Hct = 3.2%); red line: 16 red blood cells (Hct = 6.4%); black line: 44 red blood cells (Hct = 17.6%); green line: 80 red blood cells (Hct = 32%).

Figure 8

Motion of two files of 16 red blood cells (Hct = 6.4%) in the asymmetric bifurcated microchannel at time instants (a) t = 0.60 ms, (b) t = 1.21 ms, (c) t = 2.40 ms, and (d) t = 5.00 ms. Velocity vectors (upper panels) and axial velocity magnitude contours (cm/s) (lower panels) are presented. The reduced area s^* = 0.481. The spring constant of the cell membrane was k_l = k_b = 3.0 × 10⁻¹² Nm. Velocity profiles at different locations of the microvessel for different cell stiffness: (e) at the apex of the diverging bifurcation at t = 1.20 ms, (f) at the mid cross section of the bifurcation at t = 1.80 ms, (g) at the apex of the converging bifurcation at t = 2.40 ms, and (h) at the cross section 2 μm from the right outlet at t = 5.00 ms. Blue line: k_l = k_b = 3.0 × 10⁻¹³ Nm; red line: k_l = k_b = 1.0 × 10⁻¹² Nm; black line: k_l = k_b = 3.0 × 10⁻¹² Nm.

Figure 9

(a) Cell free layer thickness in the parent vessel for different hematocrit levels. (b) Separation efficiency of asymmetric bifurcated vessel for different hematocrit levels in comparison with experiments (T-channel, flow ratio = 8).