An Assessment of Six Muscle Spindle Models for Predicting Sensory Information during Human Wrist Movements

Abstract

Background: The muscle spindle is an important sensory organ for proprioceptive information, yet there have been few attempts to use Shannon information theory to quantify the capacity of human muscle spindles to encode sensory input.

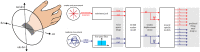
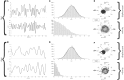
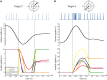
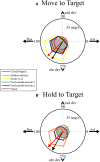
Methods: Computer simulations linked kinematics, to biomechanics, to six muscle spindle models that generated predictions of firing rate. The predicted firing rates were compared to firing rates of human muscle spindles recorded during a step-tracking (center-out) task to validate their use. The models were then used to predict firing rates during random movements with statistical properties matched to the ergonomics of human wrist movements. The data were analyzed for entropy and mutual information.

Results: Three of the six models produced predictions that approximated the firing rate of human spindles during the step-tracking task. For simulated random movements these models predicted mean rates of 16.0 ± 4.1 imp/s (mean ± SD), peak firing rates <50 imp/s and zero firing rate during an average of 25% of the movement. The average entropy of the neural response was 4.1 ± 0.3 bits and is an estimate of the maximum information that could be carried by muscles spindles during ecologically valid movements. The information about tendon displacement preserved in the neural response was 0.10 ± 0.05 bits per symbol; whereas 1.25 ± 0.30 bits per symbol of velocity input were preserved in the neural response of the spindle models.

Conclusions: Muscle spindle models, originally based on cat experiments, have predictive value for modeling responses of human muscle spindles with minimal parameter optimization. These models predict more than 10-fold more velocity over length information encoding during ecologically valid movements. These results establish theoretical parameters for developing neuroprostheses for proprioceptive function.

Keywords: Ia afferent; entropy; proprioception; sensorimotor control; spike train.

Figure 1

Schematic of the steps involved in the simulations. All simulations are hypothetical movements of the wrist in right-hand coordinates. The wrist joint coordinate system is illustrated to orient the reader to subsequent polar plot figures where angle is determined by the rotation of the wrist about its two axes. Two types of task are examined: center-out and random movements. fem, flexion/extension movement; rud, radial/ulnar deviation movement; ECRB, extensor carpi radialis brevis muscle.

Figure 2

Features of the random wrist movement simulations. (A,B) The trajectory of the random wrist movements in 2D wrist joint space is illustrated for the fastest (1.5 Hz cut-off) and slowest (0.5 Hz cut-off) movement speeds. The histograms illustrate the distribution of angles about the two wrist axis and a Gaussian curve is overlaid to illustrate the distribution of position is the same at the two different speeds. (C,D) Thirty seconds of the wrist position time series for each wrist axis to illustrate the random nature of the simulated movements. (E,F) Power spectral densities of wrist position in both wrist dimensions for the 1.5 and 0.5 Hz signals respectively.

Figure 3

Features of ECRb tendon displacement and velocity during random human wrist movements. The simulated random movements result in Gaussian distributed inputs to the muscle spindle models. The distribution of tendon displacement is constant across the slow to fast movement speeds, whereas the velocity increases. Since the simulated movements are constrained to the statistics gleaned from ergonomic studies of wrist movements, these stimuli can be considered to have a statistically natural distribution. (A,B) tendon displacement (above) and velocity (below), for fast (1.5 Hz cut-off) and slow (0.5 Hz cut-off) random wrist movements. (C,D) Histograms of tendon displacement and rectified velocity. At the faster movement, the tendon velocity distribution spreads out to higher values. (E,F) Polar plots of tendon displacement and rectified velocity (below) for 1.5 Hz (E) and 0.5 Hz (F). Positive displacement or velocity is black, negative is gray.

Figure 4

Comparing movements to opposite targets. Upper trace shows an example spike train from a human ECR muscle spindle during movements to two targets. Middle trace shows the continuous firing rate generated from the ensemble data of 8 ECR spindle afferents. The first dashed line indicates the onset of movement to the targets and the second is 650 ms later, the end of the minimum jerk movement phase.

Figure 5

Comparing the temporal dynamics of firing rate and variability for a human muscle spindle and six models. Continuous firing rate responses from a single human ECR spindle, recorded during four repeat movements to the target at 270°. A smoothed response was generated from the spike trains using a Gaussian kernel (60 ms bandwidth) and the five repeated movements were averaged to find the mean response and 95% confidence intervals (gray band). The movement duration was 662 ± 95 ms (mean, SD). Overlaid are predicted firing rates from the six models for a minimum jerk trajectory (650 ms duration) to the same target. Baseline firing rate in the models was set to 10 imp/s and the average for the human data was 8.5 imp/s. Records are aligned at movement onset (0.5 s).

Figure 6

Comparing directional tuning in polar plots. The top panel (A) shows mean firing rate for the models (see legend) and averaged human data (gray area). The preferred direction of the models (computed by mean vector) was 225° (red arrow) and the preferred direction of the human data was 239° (black arrow). The length of the normalized mean vectors (not illustrated) were: 0.28 (human), 0.28 (red), 0.46 (orange), 0.62 (yellow), 0.45 (green), 0.52 (blue), and 0.46 (purple). The bottom panel (B) shows mean firing rates during the static phase of holding on the target. Two models (yellow and green) were not significantly tuned during the hold phase (mean vector length = 0.0), while the others had the same preferred direction (225°) and normalized mean vector lengths of: 0.25 (red), 0.64 (orange), 0.28 (blue), and 0.28 (purple). The mean vector for the human data had an angle of 240° and a length of 0.11, which was significant (p < 0.05).

Figure 7

The time series and histograms of firing rates predicted for random movements. The random 2D movements in wrist joint space resulted in changes in ECRb tendon length that were input to the muscle spindle models to predict firing rates during movements of the human wrist encountered in normal movements. (A). During fast movements, the predicted firing rates are <40 imp/s. The main distinguishing feature when comparing the three models is the peak rate and periods of silence (i.e., firing rate of zero). Even during slow movements the Prochazka and Gorassini 2 model predicts periods of zero firing rate. (B). The histograms all have the same scale starting at zero firing rate and the dotted line indicates 20 imp/s. The means of these distributions, with and without using zero firing rate in the calculations, are given in Table 3. The shapes of firing rate histograms predicted by the three models are different: unimodal and bimodal. Experimental data during a similar task should be plotted in a similar fashion to evaluate the model predictions.