Disentangling Random Motion and Flow in a Complex Medium

Abstract

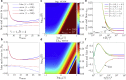
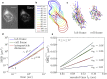
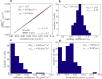
We describe a technique for deconvolving the stochastic motion of particles from large-scale fluid flow in a dynamic environment such as that found in living cells. The method leverages the separation of timescales to subtract out the persistent component of motion from single-particle trajectories. The mean-squared displacement of the resulting trajectories is rescaled so as to enable robust extraction of the diffusion coefficient and subdiffusive scaling exponent of the stochastic motion. We demonstrate the applicability of the method for characterizing both diffusive and fractional Brownian motion overlaid by flow and analytically calculate the accuracy of the method in different parameter regimes. This technique is employed to analyze the motion of lysosomes in motile neutrophil-like cells, showing that the cytoplasm of these cells behaves as a viscous fluid at the timescales examined.

Figure 1

Schematic of the BNEW method for decoupling high-frequency stochastic motion from flow, as applied to simulated particle trajectories. (a) Particles undergoing diffusive Brownian motion (red, $\alpha =1,D=5$) and subdiffusive, fractional Brownian motion (green, $\alpha =0.5,D=5$) were simulated in the presence of a flow field (black arrows), with localization error $ϵ=1$. Example trajectories are shown (from 400 total trajectories of length 200 time steps each). (b) The MSD for simulated particles. Superlinear scaling is a result of the underlying flow. Dashed lines indicate the MSD with no drift present for diffusive (red) and subdiffusive (green) motion. (c and d) Decomposition of the particle trajectories into the smoothed component (c) and the high-frequency component, ${\overrightarrow{p}}_k^{\left(n\right)}$ (d). Two high-frequency trajectories are shown for diffusive (red and magenta) and subdiffusive (green and yellow) motion. Smoothing was done using Haar wavelets with span $n=12$. (e) Adjusted MSD obtained with BNEW analysis for tracks with diffusive stochastic motion. Dashed black lines show the analytical solution (Eq. 9). (f) Rescaled adjusted MSD, as defined in Eq. 11, plotted on linear axes. Black lines indicate power-law fits to the data, with the given fit parameters. To see this figure in color, go online.

Figure 2

Errors in characterizing high-frequency stochastic motion with the BNEW method. (a) Bias and total error in the fitted scaling parameter, ${\alpha }_{\text{fit}}$, as a function of maximal wavelet span. Dashed curves give the relative bias, $\left[\langle {\alpha }_{\text{fit}}-\alpha \rangle /\alpha \right]$, and solid curves the relative error $\left[\sqrt{\langle {\left({\alpha }_{\text{fit}}-\alpha \right)}^2\rangle }/\alpha \right]$, calculated as described in Section S5, for drift correlation times of 100 time steps (blue) and 500 time steps (red). Curves shown are calculated for $\tilde{\gamma }=1,\tilde{D}=3$. (b) Corresponding curves for bias and error in $D_{\text{fit}}$. (c and d) Dependence of relative error in α_fit and D_fit on dimensionless drift magnitude, $\tilde{\gamma }$, and diffusion constant, $\tilde{D}$. All values are calculated with $\tilde{\tau }=100\text{and}{n}_{\text{max}}=17$. Dashed black lines mark a constant value of $\tilde{D}/{\tilde{\gamma }}^2$. (e and f) Relative bias (dashed curves) and error (solid curves) plotted as a function of the compound parameter, $\tilde{\tau }\tilde{D}/{\tilde{\gamma }}^2$. Persistence-time values of $10\le \tilde{\tau }\le 5000$ were used for each curve. SG-3 wavelets were used throughout, and error calculations are done for 400 tracks of length 200 time points each, assuming diffusive stochastic motion $\left(\alpha =1\right)$. Analogous calculations for the fitted localization error $\left({ϵ}_{\text{fit}}\right)$ are shown in Fig. S6. To see this figure in color, go online.

Figure 3

Comparison of error in fit parameters for high-frequency stochastic motion, using the BNEW method (solid lines) and ordinary MSD curves (dashed lines), as a function of drift magnitude, $\tilde{\gamma }$, for a constant diffusion coefficient $\tilde{D}=3$ (left panel) and as a function of diffusion coefficient, $\tilde{D}$, for a constant $\tilde{\gamma }=1$ (right panel). Drift is assumed to have a dimensionless correlation time of $\tilde{\tau }=100$. Errors shown are for 400 tracks of length 200 time steps. BNEW analysis was done using SG-3 wavelets with spans of $2\le n\le 17$. Errors for plain MSD curves were obtained from fits to $1\le k\le 3$, the smallest number of points for fitting a power law. This fitting range minimizes error in the presence of drift (see Section S7). To see this figure in color, go online.

Figure 4

Analysis of lysosome trajectories in an HL60 cell. (a) Example cell with lysotracker labeling, imaged in consecutive frames with phase contrast in addition to fluorescence (left) and with fluorescence only (right). (b) Migrating cell shape over time. (c) Example lysosome trajectories in the lab frame of reference and in the cell frame of reference. (d) Mean-squared displacement for all tracked lysosomes in the example cell, in the lab frame (blue) and the cell frame (green). The mean-squared change in interparticle distances is shown in red. Dashed lines indicate scaling as a guide to the eye. (e) Rescaled, adjusted MSD after BNEW analysis for the example cell (red), and for other representative cells (blue, green, and cyan). Wavelet smoothing was done with SG-3 wavelets for spans of $2\le n\le 17$. Black lines indicate power-law fits to Eq. 12 with the given scaling coefficients, ${\alpha }_{\text{fit}}$. To see this figure in color, go online.

Figure 5

Statistics from BNEW analysis of lysosome motion in a population of 93 HL60 cells, with an average of 391 tracks each and an average track length of 118 time steps. SG-3 wavelets with spans of $2\le n\le 17$ and time separations of $1\le k\le \lfloor 0.74n\rfloor$ were used for the BNEW analysis. (a) Rescaled MSD from BNEW analysis of all tracks pooled together. The black line shows a power-law fit with the given parameters. (b) Histogram of scaling coefficients $\left({\alpha }_{\text{fit}}\right)$ for pooled lysosome tracks from each individual cell. The population average $\left(\langle {\alpha }_{\text{fit}}\rangle \right)$ and standard deviation $\left({\sigma }_{{\alpha }_{\text{fit}}}\right)$ are as shown. (c) Histogram of diffusion coefficients $\left(D_{\text{fit}}\right)$ from individual cells. (d) Histogram of fitted localization errors $\left({ϵ}_{\text{fit}}\right)$ from individual cells. Cases with ${ϵ}_{\text{fit}}=0$ were excluded from the ensemble average and standard deviation calculations for the localization error. To see this figure in color, go online.