Somato-dendritic Synaptic Plasticity and Error-backpropagation in Active Dendrites

Abstract

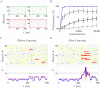
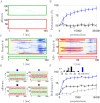
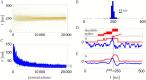
In the last decade dendrites of cortical neurons have been shown to nonlinearly combine synaptic inputs by evoking local dendritic spikes. It has been suggested that these nonlinearities raise the computational power of a single neuron, making it comparable to a 2-layer network of point neurons. But how these nonlinearities can be incorporated into the synaptic plasticity to optimally support learning remains unclear. We present a theoretically derived synaptic plasticity rule for supervised and reinforcement learning that depends on the timing of the presynaptic, the dendritic and the postsynaptic spikes. For supervised learning, the rule can be seen as a biological version of the classical error-backpropagation algorithm applied to the dendritic case. When modulated by a delayed reward signal, the same plasticity is shown to maximize the expected reward in reinforcement learning for various coding scenarios. Our framework makes specific experimental predictions and highlights the unique advantage of active dendrites for implementing powerful synaptic plasticity rules that have access to downstream information via backpropagation of action potentials.

Fig 1. Neuron model, synaptic plasticity rule and learning of spike timings.

A: Synaptic inputs targeting dendritic NMDA activation zones (A1, red endings with enlargement) propagate, together with possible NMDA-spikes, to the somatic spike trigger zone (A1, blue). Individual postsynaptic potentials in a dendritic branch (PSPs, arriving e.g. at time $t_i^{\text{pre}}$, A2), may trigger NMDA-spikes, e.g. at time $t_d^{\mathrm{d}}=5\text{ms}$ (solid) or 15 ms (dashed) after $t_i^{\text{pre}}$, forming a local dendritic plateau potential of 50 ms duration (A3). A somatic spike triggered at t^s during the ongoing NMDA-spike (A4) causes a synaptic weight change $\Delta w_{di}^{\text{sds}}$ that is large/small depending on whether the NMDA-spike was triggered 5/15 ms after the presynaptic spike (A5, solid/dashed circle, respectively). A5: $\Delta w_{di}^{\text{sds}}$ as a function of $t^s-t_i^{\text{pre}}$ for a NMDA-spike at 5 (solid) and 15 ms (dashed). B: Raster plots of freely generated somatic spikes from test trials that are interleaved with learning trials. For the full somato-dendritic synaptic plasticity rule (sdSP) the somatic spikes converge to the 3 target times with a precision of ±3 ms (top), while the rule neglecting the dendritic spikes (i.e. suppressing the term ${\dot{w}}_{di}^{\text{sds}}$) achieves a precision of only ±14 ms (bottom). C: The two spike distributions from C after 3000 presentations.

Fig 2. Binary classification of frozen input spike patterns by a somatic spike / no-spike code for the reward-modulated somato-dendritic synaptic plasticity (R-sdSP).

A: Four input patterns, the two patterns in the top row should elicit no somatic spikes; the patterns in the bottom row should. B: R-sdSP perfectly learns the classification after roughly 1000 presentations (blue solid). In contrast, classical R-STDP fails when applied to the presynaptic–somatic (‘pre-som’, solid black) or the presynaptic–dendritic (‘pre-den’, gray) spike pairs. R-STDP improves when the dendritic spike generation is suppressed (black dashed), although it does not reach the high performance of R-sdSP. C,D: Dendritic and somatic voltages in response to an input pattern that requires spiking, before (C) and after (D) learning. The initially sparse dendritic spikes (NMDA_d(t), red bars, overlaid on a $u_d^{\mathrm{d}}\left(t\right)$ intensity plot) become more numerous, co-align and sum up in the soma to enable the somatic firing. Yellow indicates depolarization. Bottom: Time course of the somatic voltage u^s(t) (blue) with the contribution of the NMDA-spikes and the somatic spike reset kernel (red).

Fig 3. R-sdSP can exploit the representational power endowed by active dendrites.

A: Example of presynaptic firing pattern that requires the neuron to be silent (green) or to elicit at least one somatic spike (red). B: R-sdSP (blue), but not R-STDP, learns to become direction selective (black: ‘pre-som’; grey: ‘pre-den’). C, D: The subthreshold dendritic voltages $u_d^{\mathrm{d}}\left(t\right)$ and NMDA traces NMDA_d(t) in response to the two input patterns shown in A (color code as in Fig 2). Individual branches developed direction selectivity (green). Bottom: action potentials are only generated for one direction. E: The 4 input patterns of the linearly non-separable feature-binding problem combine one of two shapes (‘circle’ or ‘diamond’) with one of two fill colors (‘blue’ or ‘black’). Each of the four features is represented by 25 afferents (next to the corresponding symbol on the y-axes) that encode its presence or absence by a high (40Hz) or low (5Hz) Poisson firing rate, respectively. F: R-sdSP learns the correct response to the 4 inputs, R-STDP does not (line code as above). Inset: average performance of each run after learning.

Fig 4. R-sdSP learns exact somatic spike timing.

A: Somatic spike trains during 20000 trials in a reward based scenario. B: The distribution of somatic spikes after learning of the target time at 250 ms has a Gaussian half-width of 18 ms. C: Evolution of the width (σ) of the spike-time distribution during training. D,E: Separation of the somatic voltage into a contribution from the NMDA-spikes (red) and the subthreshold dendritic potentials (blue) for a single run (D) and averaged across 20 runs (E). Note that after learning the summed NMDA-spikes can form a narrow depolarizations at the target time beyond the duration of an individual spike (arrow in D).

Fig 5. R-sdSP learns the correct spike-timing in a navigational task with binary and delayed feedback.

A: At each position a fixed spike pattern is presented, and the timing of the first somatic spike tells how many steps in the clock (−) or counter clock (+) direction are taken. Color code of the time bin indicates the preferred spike timing for directly jumping to target position 0 when being at the correspondingly colored circle position (see text). B: Evolution of the mean number of jumps needed from a randomly chosen circle position until 0 is reached. C: Performance Index defined as the probability of directly jumping from any of the 6 circle positions to the target, and staying there if already at 0. Before learning this probability is 0.13, after learning it is 0.78. D: Histogram of first somatic spikes at the various positions before and after learning, averaged across patterns and learning runs (color code as in A). (E) Timing of the first NMDA spike in each of the 20 branches (upper panel) and the first somatic spike (lower panel) when stimulated with the patterns associated to the 6 circle positions (colors encode positions as in A). After learning, NMDA-spikes in 2-4 branches co-align and trigger somatic spike timing the appropriate time bin.