Metainference: A Bayesian inference method for heterogeneous systems
- PMID: 26844300
- PMCID: PMC4737209
- DOI: 10.1126/sciadv.1501177
Metainference: A Bayesian inference method for heterogeneous systems
Abstract
Modeling a complex system is almost invariably a challenging task. The incorporation of experimental observations can be used to improve the quality of a model and thus to obtain better predictions about the behavior of the corresponding system. This approach, however, is affected by a variety of different errors, especially when a system simultaneously populates an ensemble of different states and experimental data are measured as averages over such states. To address this problem, we present a Bayesian inference method, called "metainference," that is able to deal with errors in experimental measurements and with experimental measurements averaged over multiple states. To achieve this goal, metainference models a finite sample of the distribution of models using a replica approach, in the spirit of the replica-averaging modeling based on the maximum entropy principle. To illustrate the method, we present its application to a heterogeneous model system and to the determination of an ensemble of structures corresponding to the thermal fluctuations of a protein molecule. Metainference thus provides an approach to modeling complex systems with heterogeneous components and interconverting between different states by taking into account all possible sources of errors.
Keywords: Statistical inference; maximum entropy principle; structural biology.
Figures
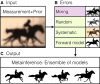
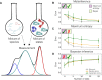
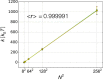
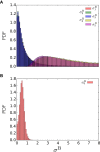

References
-
- G. E. Box, G. C. Tiao, Bayesian Inference in Statistical Analysis (John Wiley & Sons, New York, 2011), vol. 40.
-
- Bernardo J. M., Smith A. F., Bayesian Theory (John Wiley & Sons, New York, 2009), vol. 405.
-
- P. M. Lee, Bayesian Statistics: An Introduction (John Wiley & Sons, New York, 2012).
-
- Jaynes E. T., Information theory and statistical mechanics. Phys. Rev. 106, 620–630 (1957).
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources

