Non-parametric combination and related permutation tests for neuroimaging
- PMID: 26848101
- PMCID: PMC4783210
- DOI: 10.1002/hbm.23115
Non-parametric combination and related permutation tests for neuroimaging
Abstract
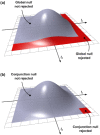
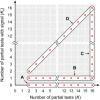
In this work, we show how permutation methods can be applied to combination analyses such as those that include multiple imaging modalities, multiple data acquisitions of the same modality, or simply multiple hypotheses on the same data. Using the well-known definition of union-intersection tests and closed testing procedures, we use synchronized permutations to correct for such multiplicity of tests, allowing flexibility to integrate imaging data with different spatial resolutions, surface and/or volume-based representations of the brain, including non-imaging data. For the problem of joint inference, we propose and evaluate a modification of the recently introduced non-parametric combination (NPC) methodology, such that instead of a two-phase algorithm and large data storage requirements, the inference can be performed in a single phase, with reasonable computational demands. The method compares favorably to classical multivariate tests (such as MANCOVA), even when the latter is assessed using permutations. We also evaluate, in the context of permutation tests, various combining methods that have been proposed in the past decades, and identify those that provide the best control over error rate and power across a range of situations. We show that one of these, the method of Tippett, provides a link between correction for the multiplicity of tests and their combination. Finally, we discuss how the correction can solve certain problems of multiple comparisons in one-way ANOVA designs, and how the combination is distinguished from conjunctions, even though both can be assessed using permutation tests. We also provide a common algorithm that accommodates combination and correction.
Keywords: conjunctions; general linear model; multiple testing; non-parametric combination; permutation tests.
© 2016 The Authors Human Brain Mapping Published by Wiley Periodicals, Inc.
Figures


References
-
- Anderson TW (2003): An Introduction to Multivariate Statistical Analysis. Hoboken, NJ: Wiley.
-
- Benjamini Y, Hochberg Y (1995): Controlling the false discovery rate: A practical and powerful approach to multiple testing. J R Stat Soc Ser B 57:289–300.
-
- Benjamini Y, Heller R (2008): Screening for partial conjunction hypotheses. Biometrics 64:1215–1222. - PubMed
-
- Berger RL (1982): Multiparameter hypothesis testing and acceptance sampling. Technometrics 24:295–300.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Miscellaneous

