Method to represent the distribution of QTL additive and dominance effects associated with quantitative traits in computer simulation

Abstract

Background: Computer simulation is a resource which can be employed to identify optimal breeding strategies to effectively and efficiently achieve specific goals in developing improved cultivars. In some instances, it is crucial to assess in silico the options as well as the impact of various crossing schemes and breeding approaches on performance for traits of interest such as grain yield. For this, a means by which gene effects can be represented in the genome model is critical.

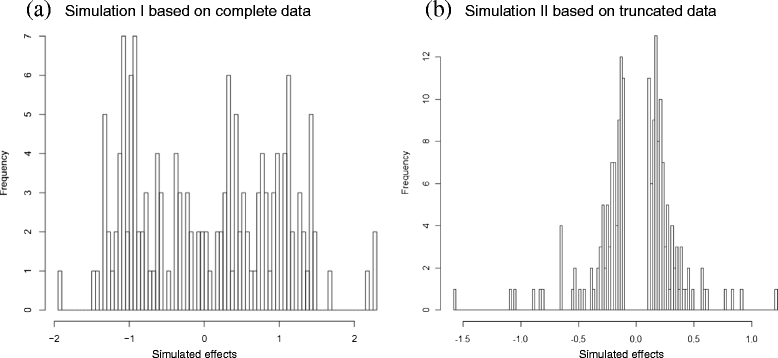
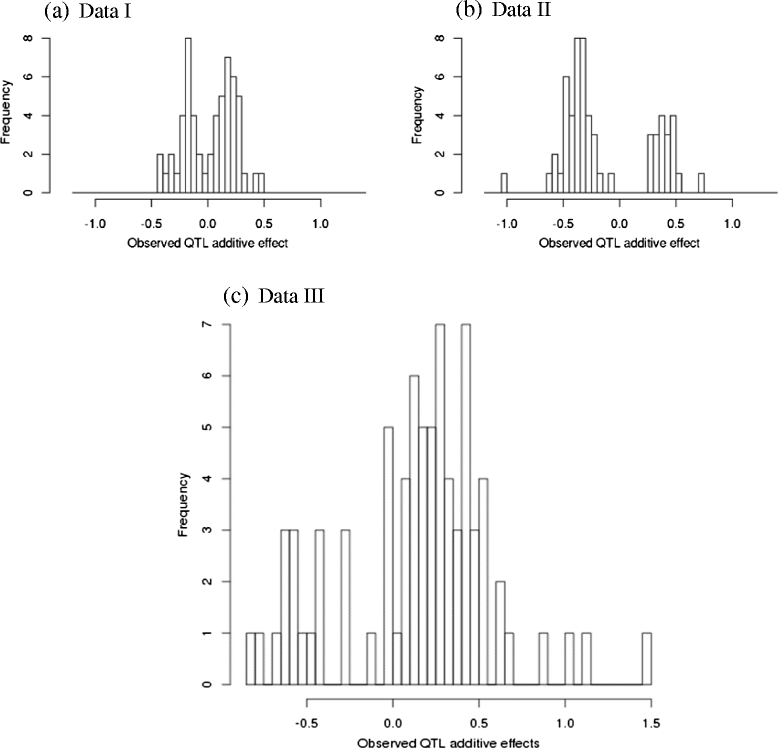
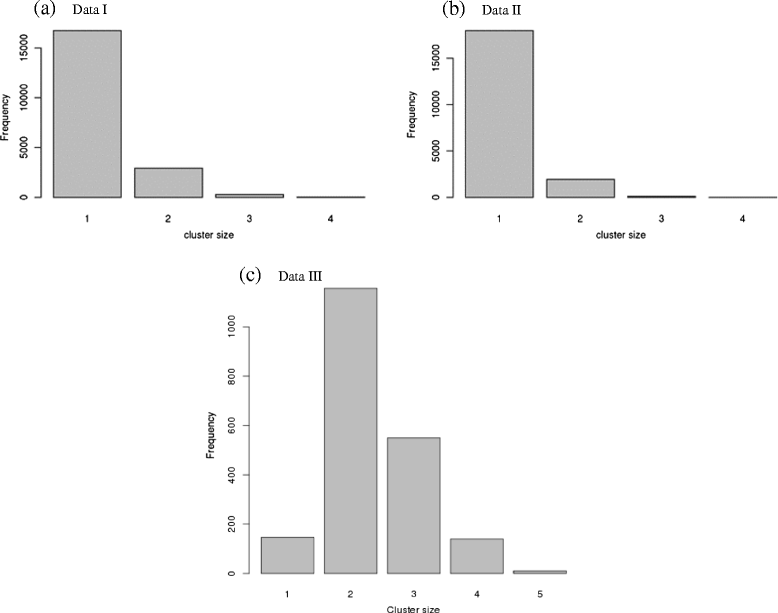
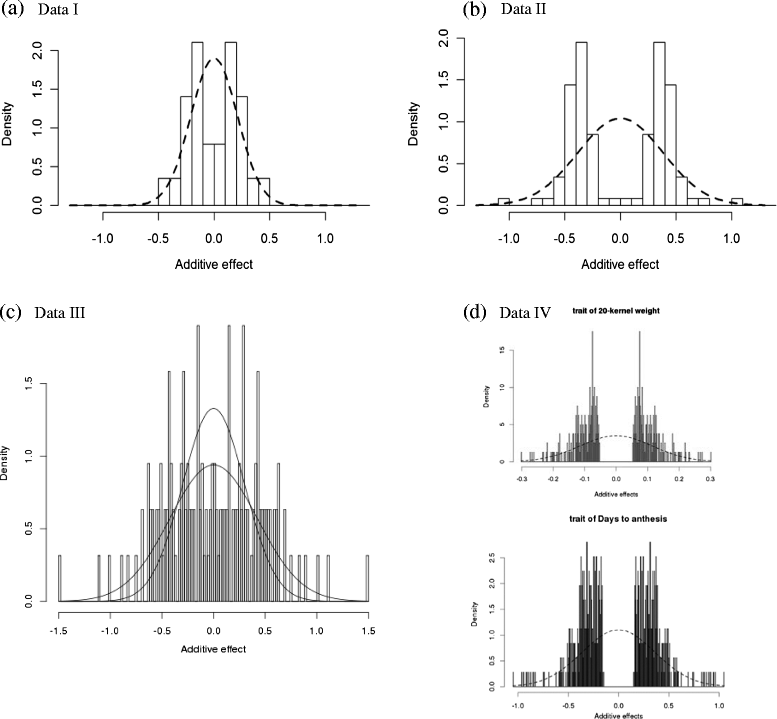
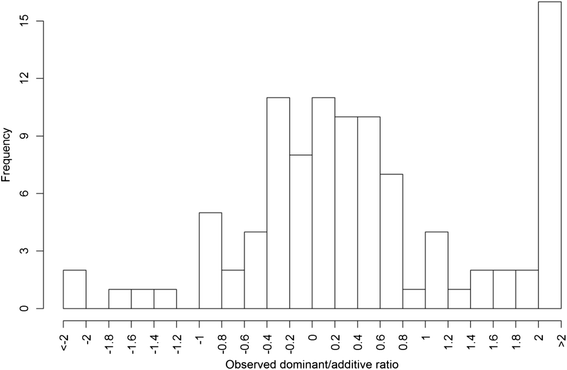
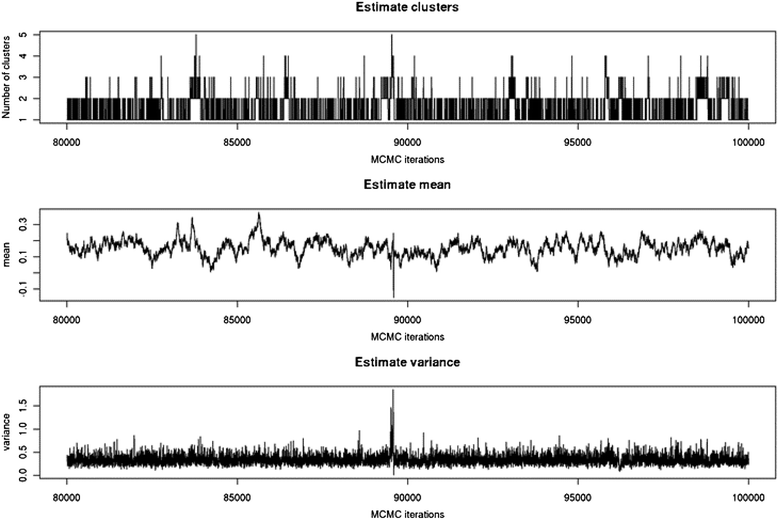
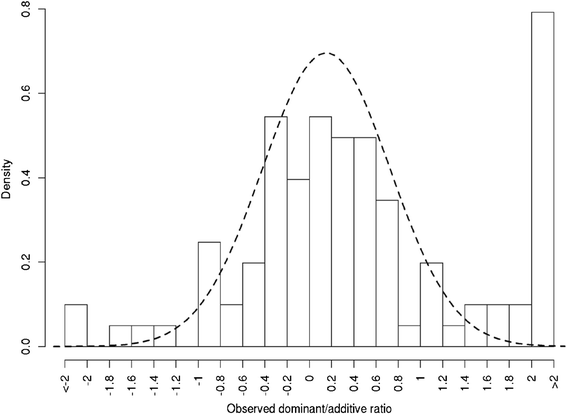
Results: To address this need, we devised a method to represent the genomic distribution of additive and dominance gene effects associated with quantitative traits. The method, based on meta-analysis of previously-estimated QTL effects following Bennewitz and Meuwissen (J Anim Breed Genet 127:171-9, 2010), utilizes a modified Dirichlet process Gaussian mixture model (DPGMM) to fit the number of mixture components and estimate parameters (i.e. mean and variance) of the genomic distribution. The method was demonstrated using several maize QTL data sets to provide estimates of additive and dominance effects for grain yield and other quantitative traits for application in maize genome simulations.

Conclusions: The DPGMM method offers an alternative to the over-simplified infinitesimal model in computer simulation as a means to better represent the genetic architecture of quantitative traits, which likely involve some large effects in addition to many small effects. Furthermore, it confers an advantage over other methods in that the number of mixture model components need not be known a priori. In addition, the method is robust with use of large-scale, multi-allelic data sets or with meta-analyses of smaller QTL data sets which may be derived from bi-parental populations in precisely estimating distribution parameters. Thus, the method has high utility in representing the genetic architecture of quantitative traits in computer simulation.

Fig. 1

Histograms of simulated effects from Gaussian mixtures: a (n = 150) three components having mean of -1, 0 and 1, and variance of 0.36, 0.64 and 0.04, respectively, and equal mixing proportions for all three components; and (b) (n = 300) two components having zero means and variance of 0.023 and 0.36, respectively, and mixing proportions of 0.8 and 0.2, respectively. Distribution in (b) is truncated at points -0.1 and 0.1

Fig. 2

Histograms of observed QTL additive effects (expressed in units of phenotypic standard deviation): a Data I; b Data II; and c Data III

Fig. 3

Histograms of the cluster number: a Data I; b Data II; and c Data III

Fig. 4

Fitted normal distributions to QTL additive effects (expressed in units of phenotypic standard deviation): a Data I; b Data II; c Data III; d Data IV featuring traits of 20-kernel weight and days to anthesis

Fig. 5

Histogram of observed dominance coefficients from meta-analysis based on five mapping populations

Fig. 6

Estimation of cluster number, mean, and variance of the fitted distribution of dominance coefficients through MCMC

Fig. 7

Normal distribution fitted to the dominance coefficients, with estimated mean at 0.152 with 95 % Bayesian confidence interval to be 0.055 and 0.237 and estimated variance at 0.329 with 95 % Bayesian confidence interval to be 0.193 and 0.542