Modeling of Soft Tissues Interacting with Fluid (Blood or Air) Using the Immersed Finite Element Method

Abstract

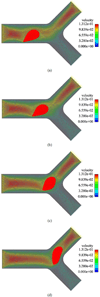
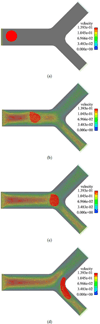
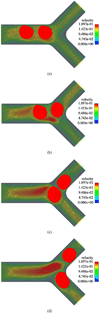
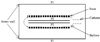
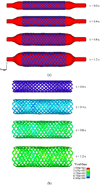
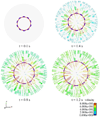
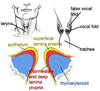
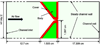
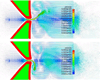
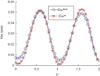
This paper presents some biomedical applications that involve fluid-structure interactions which are simulated using the Immersed Finite Element Method (IFEM). Here, we first review the original and enhanced IFEM methods that are suitable to model incompressible or compressible fluid that can have densities that are significantly lower than the solid, such as air. Then, three biomedical applications are studied using the IFEM. Each of the applications may require a specific set of IFEM formulation for its respective numerical stability and accuracy due to the disparities between the fluid and the solid. We show that these biomedical applications require a fully-coupled and stable numerical technique in order to produce meaningful results.

Keywords: Biomechanics; Fluid-Structure Interactions.

Figure 1

Computational domain decomposition.

Figure 2

Bifurcation geometry.

Figure 3

A RBC owing in a symmetric bifurcated vessel with Q₁/Q₂ = 3. (a) t = 0.008 s; (b) t = 0.012 s; (c) t =0.016 s; (d) t = 0.020 s.

Figure 4

A RBC flowing in an asymmetric bifurcation vessel with Q₁/Q₂ =1. (a) t = 0.00 s; (b) t = 0.01 s; (c) t =0.02 s; (d) t = 0.03 s.

Figure 5

Two RBCs in a symmetric bifurcation. (a) t = 0.004 s; (b) t = 0.008 s; (c) t =0.012 s; (d) t = 0.018 s.

Figure 6

Balloon geometry setup. (a) Initial balloon geometry before inflation; (b) Fixed boundaries applied at the two ends of the balloon.

Figure 7

Design of a Medtronic AVE Modular stents S7.

Figure 8

Initial configuration of catheter, ballon, and stent.

Figure 9

The initial conditions applied to the fluid domain: constant pressure difference (P₂ − P₁) is applied from the catheter to the fluid boundaries.

Figure 10

Stent configuration and von Mises stress map during stent deployment. (a) Stent deployment process; (b) Von Mises stress during stent deployment.

Figure 11

Stent diameter and maximum von Mises stress vs. time during stent deployment. (a) Stent diameter variation during the deployment; (b) Maximum Von Mises stress variation during the deployment.

Figure 12

Radial fluid velocity profile at different time steps.

Figure 13

Velocity profile in the longitudinal direction during expansion at different time steps.

Figure 14

Human vocal folds.

Figure 15

2-D two-layer self-oscillated vocal folds model.

Figure 16

Fluid velocity field at two typical instances during steady vibration.

Figure 17

Half glottis width of top and bottom vocal folds.

Figure 18

Spectrum plot of flow rate and half glottis width of the top and bottom vocal folds.