Modelling of bone fracture and strength at different length scales: a review
- PMID: 26855749
- PMCID: PMC4686238
- DOI: 10.1098/rsfs.2015.0055
Modelling of bone fracture and strength at different length scales: a review
Abstract
In this paper, we review analytical and computational models of bone fracture and strength. Bone fracture is a complex phenomenon due to the composite, inhomogeneous and hierarchical structure of bone. First, we briefly summarize the hierarchical structure of bone, spanning from the nanoscale, sub-microscale, microscale, mesoscale to the macroscale, and discuss experimental observations on failure mechanisms in bone at these scales. Then, we highlight representative analytical and computational models of bone fracture and strength at different length scales and discuss the main findings in the context of experiments. We conclude by summarizing the challenges in modelling of bone fracture and strength and list open topics for scientific exploration. Modelling of bone, accounting for different scales, provides new and needed insights into the fracture and strength of bone, which, in turn, can lead to improved diagnostic tools and treatments of bone diseases such as osteoporosis.
Keywords: bone fracture; bone strength; computational modelling; hierarchical structure; multiscale modelling.
Figures


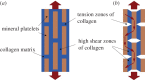

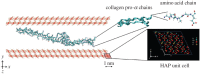

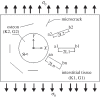
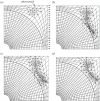

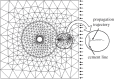

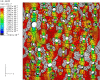

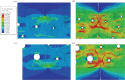
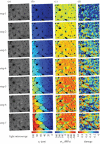


References
-
- Olszta MJ, Cheng X, Soo Jee S, Kumar R, Kim Y-Y, Kaufman MJ, Douglas EP, Gower LB. 2007. Bone structure and formation: a new perspective. Mater. Sci. Eng. R 58, 77–116. ( 10.1016/j.mser.2007.05.001) - DOI
-
- Novitskaya E, Po-Yu C, Elham H, Li J, Vlado L, Iwona J, Joanna M. 2011. Recent advances on the measurement and calculation of the elastic moduli of cortical and trabecular bone: a review. Theor. Appl. Mech. 38, 209–297. ( 10.2298/TAM1103209N) - DOI
-
- Jackson SA, Cartwright AG, Lewis D. 1978. Morphology of bone-mineral crystals. Cacif. Tissue Int. 25, 217–222. - PubMed
LinkOut - more resources
Full Text Sources
Other Literature Sources

