On the Use of Bone Remodelling Models to Estimate the Density Distribution of Bones. Uniqueness of the Solution

Abstract

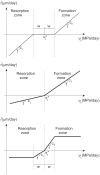
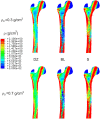
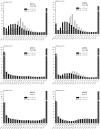
Bone remodelling models are widely used in a phenomenological manner to estimate numerically the distribution of apparent density in bones from the loads they are daily subjected to. These simulations start from an arbitrary initial distribution, usually homogeneous, and the density changes locally until a bone remodelling equilibrium is achieved. The bone response to mechanical stimulus is traditionally formulated with a mathematical relation that considers the existence of a range of stimulus, called dead or lazy zone, for which no net bone mass change occurs. Implementing a relation like that leads to different solutions depending on the starting density. The non-uniqueness of the solution has been shown in this paper using two different bone remodelling models: one isotropic and another anisotropic. It has also been shown that the problem of non-uniqueness is only mitigated by removing the dead zone, but it is not completely solved unless the bone formation and bone resorption rates are limited to certain maximum values.

Fig 1. Different RRR analyzed: (a) with dead zone (DZ), (b) bilinear (BL), (c) with saturation (S).

Fig 2. FE model of the femur and location of the insertion points of the muscles (red); point of application of the resultant of hip reaction (yellow).

Fig 3. Distribution of density obtained in a frontal section of the femur in the cases that implemented IBRM.

Fig 4. Distribution of density obtained in a frontal section of the femur in the cases that implemented ABRM.

Fig 5. Histograms with the occurrence of density in the elements of the femur. The groups are named after their range of apparent density (g/cm³).