Influence of Global and Local Membrane Curvature on Mechanosensitive Ion Channels: A Finite Element Approach

Abstract

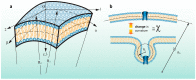
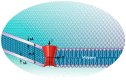
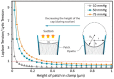
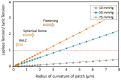
Mechanosensitive (MS) channels are ubiquitous molecular force sensors that respond to a number of different mechanical stimuli including tensile, compressive and shear stress. MS channels are also proposed to be molecular curvature sensors gating in response to bending in their local environment. One of the main mechanisms to functionally study these channels is the patch clamp technique. However, the patch of membrane surveyed using this methodology is far from physiological. Here we use continuum mechanics to probe the question of how curvature, in a standard patch clamp experiment, at different length scales (global and local) affects a model MS channel. Firstly, to increase the accuracy of the Laplace's equation in tension estimation in a patch membrane and to be able to more precisely describe the transient phenomena happening during patch clamping, we propose a modified Laplace's equation. Most importantly, we unambiguously show that the global curvature of a patch, which is visible under the microscope during patch clamp experiments, is of negligible energetic consequence for activation of an MS channel in a model membrane. However, the local curvature (RL < 50) and the direction of bending are able to cause considerable changes in the stress distribution through the thickness of the membrane. Not only does local bending, in the order of physiologically relevant curvatures, cause a substantial change in the pressure profile but it also significantly modifies the stress distribution in response to force application. Understanding these stress variations in regions of high local bending is essential for a complete understanding of the effects of curvature on MS channels.

Keywords: continuum mechanics; finite element; local bending; mechanosensitive ion channel; membrane local curvature.

Figure 1

The difference between local and global curvature. Change in global (R_G) and local (R_L) radius of curvature of a membrane patch from a ‘resting state’ to an inflated dome state during applied negative pressure. The regions causing local curvature here in a biological membrane (e.g., caveolae) are of course not seen in a ‘pure’ lipid bilayer. As pressure is applied the regions of high local curvature flatten out. In a cellular environment this flattening of caveolae provides a degree of mechanoprotection by buffering the membrane tension in response to an applied force.

Figure 2

Schematic of membrane curvature. (a) An element of a membrane patch where the principal coordinates, Lamé parameters, radii of curvature, R1 and R2, change in curvature terms, ${\chi }_1$ and ${\chi }_2$ are shown. $\mathsf{\alpha }$ and $\mathsf{\beta }$ are lines of curvature in the curvilinear coordinates; (b) Schematic description of the “change” in curvature term. This parameter, $\chi$, is the change in curvature from the bilayer mid-plane between two different states.

Figure 3

The FE model of the lipid bilayer and the incorporated MscL. The upper and lower layers represent the head groups and the core illustrates the tails of lipid bilayer. The thickness of the representative volume element (RVE) is 5 Å.

Figure 4

The effect of the flattening of the patch on the ratio of the membrane tension distribution and the lytic tension (calculated using the Laplace equation).

Figure 5

The effect of the radius of curvature on ratio of the distributed tension and the lytic tension. By decreasing the radius of curvature to the RHLC (Region of High Local Curvature), the calculated tension using the simplified form of the Laplace’s law approaches zero. This implies that all of the channels in RHLC don’t sense the membrane tension produced by the applied negative pressure.

Figure 6

High-resolution images of a cell-attached patch containing G22S-MscL-cGFP channels and corresponding current activated during steps of negative pressure. (a) Images of a cell-attached membrane patch from a HEK293T cell; (b) Activation of G22S-MscL-cGFP channels by increasing 2s pressure steps from −25 to −75 mmHg (ΔV_patch = +5 mV); (c) Comparison between radius of curvature, R_c, of Laplace equation and equivalent radius of curvature, R_equ, used in our modified Laplace’s equation. This R_equ is more adequate for estimating the tension distribution in semi-flat states of the membrane patch as well as other patch clamping situations; (d) Calculation of stress induced by suction in all 6 stages of patch clamping using different techniques [42,43] (e). Open probability of G22S-MscL-cGFP channels from record (b) plotted against the tension calculated using different methods [42,43].

Figure 7

Stress distribution along the membrane thickness in response to outward bending (outward bending). (a) Schematic stress distribution along the channel in the lipid bilayer showing two distinct regions, which experience compressive and tensile stress; (b) Normal stress (${\mathsf{\sigma }}_x$) distribution due to the local curvature and superposition of suction pressure of 20, 40 and 60 mmHg for a radius of curvature of R_L = 25 nm and (c) radius of curvature R_L = 15 nm. The red line in both illustrates the stress distribution in the presence of global curvature R_G = 2.5 μm alone while the blue line represents global curvature superimposed on 60 mmHg applied pressure. The pressure profile is the opposite under inward bending.

Figure 8

Change in the pressure profile along the membrane thickness due to the application of two levels of local curvature (Outward bending). This is equivalent to the curvature seen upon PLC activation, which cleaves PIP2 in the inner bilayer leaflet to produce diacylglycerol (DAG), which in turn can change local curvature of the membrane. This curvature also mimics the addition of lysophosphatidylcholine (LPC) or a similar shaped lipid into the outer leaflet. The opposite is true for negative curvature in this situation.

Figure 9

Schematic representation of how local bending can have different effects on gating of structurally different channels (Channel A and Channel B). If we assume both channels are in the closed state (a); bending of the membrane in the inward direction (b); tends to open Channel A but close Channel B. Conversely, applying local bending in the outward direction (c) tends to close Channel A and open Channel B.