Kinetics of cellular uptake of viruses and nanoparticles via clathrin-mediated endocytosis
- PMID: 26871680
- PMCID: PMC6748044
- DOI: 10.1088/1478-3975/13/1/016005
Kinetics of cellular uptake of viruses and nanoparticles via clathrin-mediated endocytosis
Abstract
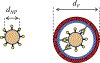
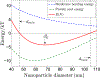
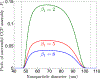
Several viruses exploit clathrin-mediated endocytosis to gain entry into host cells. This process is also used extensively in biomedical applications to deliver nanoparticles (NPs) to diseased cells. The internalization of these nano-objects is controlled by the assembly of a clathrin-containing protein coat on the cytoplasmic side of the plasma membrane, which drives the invagination of the membrane and the formation of a cargo-containing endocytic vesicle. Current theoretical models of receptor-mediated endocytosis of viruses and NPs do not explicitly take coat assembly into consideration. In this paper we study cellular uptake of viruses and NPs with a focus on coat assembly. We characterize the internalization process by the mean time between the binding of a particle to the membrane and its entry into the cell. Using a coarse-grained model which maps the stochastic dynamics of coat formation onto a one-dimensional random walk, we derive an analytical formula for this quantity. A study of the dependence of the mean internalization time on NP size shows that there is an upper bound above which this time becomes extremely large, and an optimal size at which it attains a minimum. Our estimates of these sizes compare well with experimental data. We also study the sensitivity of the obtained results on coat parameters to identify factors which significantly affect the internalization kinetics.
Figures

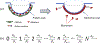



References
-
- Iversen TG, Skotland T and Sandvig K 2011. Endocytosis and intracellular transport of nanoparticles: present knowledge and need for future studies Nano Today 6 176–85
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Miscellaneous
