Using MD Simulations To Calculate How Solvents Modulate Solubility

Abstract

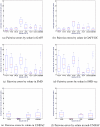
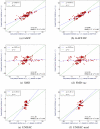
Here, our interest is in predicting solubility in general, and we focus particularly on predicting how the solubility of particular solutes is modulated by the solvent environment. Solubility in general is extremely important, both for theoretical reasons - it provides an important probe of the balance between solute-solute and solute-solvent interactions - and for more practical reasons, such as how to control the solubility of a given solute via modulation of its environment, as in process chemistry and separations. Here, we study how the change of solvent affects the solubility of a given compound. That is, we calculate relative solubilities. We use MD simulations to calculate relative solubility and compare our calculated values with experiment as well as with results from several other methods, SMD and UNIFAC, the latter of which is commonly used in chemical engineering design. We find that straightforward solubility calculations based on molecular simulations using a general small-molecule force field outperform SMD and UNIFAC both in terms of accuracy and coverage of the relevant chemical space.

Figure 1

2D structures for all solute and solvent molecules. The corresponding CIDs are showing on the left upper corner of each panel.

Figure 2

The average error in $\text{ln}\left(\frac{c_1^{\alpha }}{c_1^{\zeta }}\right)$ by solute, across all possible solvent pairs for each solute for the different methods considered (a-f). The vertical axis shows the error in the log ratio (unitless), and the horizontal axis shows the solvent considered. The plot is a box and whisker plot, with the box showing the lower and upper quartiles of the data, and the red line marking the median. The whiskers show the range of the data.

Figure 3

Comparison of calculated relative solubilities with the experimental relative solubilities for all solute-solvent pairs and all methods.

Figure 4

Comparison of errors for different methods for each solute in all pairs of solvents. The x = y line divides the figure into two regions, the left-top region and right-bottom region. If a particular datapoint is in the left-top region, then the method shown on the x-axis performs better for that particular case, and if the point is in the right-bottom region, the method shown on the y-axis performs better.

Figure 5

An example of how we calculate the test and training set errors. Here, we examine a particular solute (A) in three solvents (B-D). As discussed in the text, we pick one particular solvent (B) in which to “predict” the solubility of the compound, and use the other solvents to calculate the best estimate of the fugacity (f_ave) of the solute by comparison to the experimental solubilities. From this estimate, we can then calculate solubility of the solute in solvent B, or (nearly equivalently) the fugacity term for B. This allows us to calculate the error in the fugacity for our test case, B (the test set error), and the error in the fugacity for the other cases (the training set error).