A Finite Element Model Approach to Determine the Influence of Electrode Design and Muscle Architecture on Myoelectric Signal Properties

Abstract

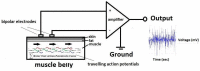
Introduction: Surface electromyography (sEMG) is the measurement of the electrical activity of the skeletal muscle tissue detected at the skin's surface. Typically, a bipolar electrode configuration is used. Most muscles have pennate and/or curved fibres, meaning it is not always feasible to align the bipolar electrodes along the fibres direction. Hence, there is a need to explore how different electrode designs can affect sEMG measurements.

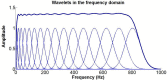
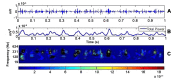
Method: A three layer finite element (skin, fat, muscle) muscle model was used to explore different electrode designs. The implemented model used as source signal an experimentally recorded intramuscular EMG taken from the biceps brachii muscle of one healthy male. A wavelet based intensity analysis of the simulated sEMG signal was performed to analyze the power of the signal in the time and frequency domain.

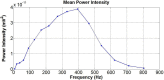
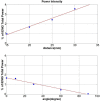
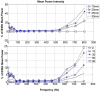
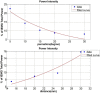
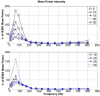
Results: The model showed muscle tissue causing a bandwidth reduction (to 20-92- Hz). The inter-electrode distance (IED) and the electrode orientation relative to the fibres affected the total power but not the frequency filtering response. The effect of significant misalignment between the electrodes and the fibres (60°-90°) could be reduced by increasing the IED (25-30 mm), which attenuates signal cancellation. When modelling pennated fibres, the muscle tissue started to act as a low pass filter. The effect of different IED seems to be enhanced in the pennated model, while the filtering response is changed considerably only when the electrodes are close to the signal termination within the model. For pennation angle greater than 20°, more than 50% of the source signal was attenuated, which can be compensated by increasing the IED to 25 mm.

Conclusion: Differences in tissue filtering properties, shown in our model, indicates that different electrode designs should be considered for muscle with different geometric properties (i.e. pennated muscles).

Fig 1. A typical Bipolar configuration scheme.

Measurements are made as the difference between the signals of two sensing electrodes, separated by a known distance. The detected signal is the sum of the action potentials (MUAPs) travelling along the fibres.

Fig 2

(Left) Three layers FEM of the muscle tissue. The simulated model consisted of an intramuscular travelling potential which generated a potential on the surface of the model. The surface potential is then detected by two probe areas representing the electrodes. These probes record the average potential over the area, reflecting the behaviour of sEMG electrodes. The coloured bar represents the tissue electric potential. (Right) FEM four node tetrahedral mesh. A finer mesh was built in the electrodes areas.

Fig 3. Representations of some of the bipolar configurations simulated, showing:.

A) inter-electrode distances (mm); B) electrodes orientation (Degree); C) fibre pennation angle (Degree). The signal travels along the horizontal plane in the muscle tissue at a depth of 20 mm. For the pennated case, the plane is inclined at different angles.

Fig 4. The 16 wavelets set in the frequency domain.

The sum of the wavelet (thick line) gives the total band of the filter. Each peak is the central frequency of the single wavelet.

Fig 5. The source signal power in time and frequency domain.

The 1 sec sample from intramuscular signal that was used as source signal is shown at the top (A). The total power of this signal is shown in the time domain (B) and in the frequency-time domain (C). From this plot it is possible to distinguish bursts of activity that occur during the isometric contraction. These are represented by high frequency peaks in the time domain, amplitude peaks in the power plot and red yellow region in the time-frequency domain. It can be seen that the power peaks are mainly at higher frequencies.

Fig 6. The source signal mean power.

The source signal mean power over 1 sec calculated for each frequency component of the source signal.

Fig 7. Total Power expressed as percentage of the source signal total power.

(Top) Total power for different IED, showing a positive linear trend as the distance is increasing (Bottom) Total Power at different orientation, showing a decay as the electrodes alignment deviate from 0° to 90°.

Fig 8. Mean Power of the bipolar signal in the frequency domain.

The general trend reveal a band stop filtering in the range 92–542 Hz (Top) Mean power at different IED. As the distance increases, the mean power increases as well. (Bottom) Mean power at different orientations. As the electrodes deviate from the direction of the signal, the mean power decreases, until reaching almost zero at 90°.

Fig 9. Total Power of the bipolar configuration.

(Top) Total power at different fibre pennation angles. There is a linear decrease of the power as the pennation increase for a fixed IED of 20 mm. (Bottom) Total Power for a pennated model at 20° while changing the IED. The increase in the power as the distance increase is almost double as that found in the parallel fibres model.

Fig 10. Mean Power of the bipolar signal in the pennated case.

(Top) The mean power at different pennation is low pass filtered and the amplitude increase as the pennation decrease. (Bottom) Mean power for the pennated case at 20° while changing the IED (15,20,25,30 mm). There is an enhanced peak for the IED of 30 mm for which the electrodes are close to the terminating point.