Clustering Genes of Common Evolutionary History

Abstract

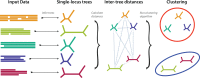
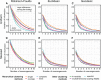
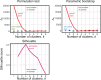
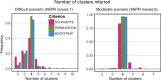
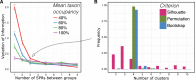
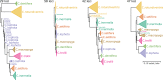
Phylogenetic inference can potentially result in a more accurate tree using data from multiple loci. However, if the loci are incongruent-due to events such as incomplete lineage sorting or horizontal gene transfer-it can be misleading to infer a single tree. To address this, many previous contributions have taken a mechanistic approach, by modeling specific processes. Alternatively, one can cluster loci without assuming how these incongruencies might arise. Such "process-agnostic" approaches typically infer a tree for each locus and cluster these. There are, however, many possible combinations of tree distance and clustering methods; their comparative performance in the context of tree incongruence is largely unknown. Furthermore, because standard model selection criteria such as AIC cannot be applied to problems with a variable number of topologies, the issue of inferring the optimal number of clusters is poorly understood. Here, we perform a large-scale simulation study of phylogenetic distances and clustering methods to infer loci of common evolutionary history. We observe that the best-performing combinations are distances accounting for branch lengths followed by spectral clustering or Ward's method. We also introduce two statistical tests to infer the optimal number of clusters and show that they strongly outperform the silhouette criterion, a general-purpose heuristic. We illustrate the usefulness of the approach by 1) identifying errors in a previous phylogenetic analysis of yeast species and 2) identifying topological incongruence among newly sequenced loci of the globeflower fly genus Chiastocheta We release treeCl, a new program to cluster genes of common evolutionary history (http://git.io/treeCl).

Keywords: clustering; incomplete lineage sorting.; incongruence; nonorthology; phylogeny; process-agnostic.

Fig. 1.

Overview of the clustering process. From left to right: input alignments are read; trees are inferred from the alignments; intertree distances are computed and used as the basis for clustering. Further procedures are used to re-estimate one tree for each cluster and to choose the optimal number of clusters—see text for details.

Fig. 2.

The relative performances of combinations of distance metric (varying over columns of panels) and clustering methods (shown by the colors of the lines), as measured by the variation of information metric (y-axes; higher values show a larger departure from the correct solution). Lines show the mean value obtained from 1,000 replicates, and the error bars show the standard error of the mean. Rows correspond to the experiments with a partition of uniformly sized clusters (A–C) and those with a partition of clusters of skewed sizes (D–F). In each individual panel, the x-axis represents the number of NNI rearrangements separating the underlying clusters, so that increasing values along this axis correlate with the clustering problem becoming easier.

Fig. 3.

Comparison of the criteria used to determine the number of clusters on a single problem instance—in this example, data simulated for 60 loci belonging to 4 clusters, each of size 15, with the clusters’ trees separated by 1 SPR. As the proposed number of clusters increases, the likelihood increases, which is expected because of the greater number of free parameters in the model. (A) Permutation test: the improvement in likelihood for each additional cluster (red curve) is significantly greater than that observed for permuted data sets (green dots show the distribution of values over 100 permutations) until the comparison between four and five clusters is reached, correctly implying that the use of four clusters is optimal. (B) Parametric bootstrap test: again, the improvement for each additional cluster (red curve) is significantly greater than that for data sets simulated for one fewer cluster (blue dots) until the true number of clusters (four) has been reached. (C) Silhouette score: the general-purpose silhouette stopping criterion has its maximum at the true value of 4. We note that in this instance, comprising a single data set from one simulation design, the three methods agree on the true answer.

Fig. 4.

Aggregate results for 400 difficult problem instances (left) and 400 moderate instances (right). The true number of clusters is 4. In both sets, our new stopping criteria (permutation and bootstrap) perform better than the general-purpose silhouette method.

Fig. 5.

(A) Distance of the spectral clustering of geodesic distances from the “true” clustering for varying levels of taxon occupancy. Just as with complete groups, partial groups converge to the correct assignment as the distance between clusters increases. When clusters differ from the underlying species tree by three SPRs or more, the effect of incomplete occupancy on performance is very slight. (B) Effect of incomplete taxon occupancy on cluster number selection criteria. Nonparametric permutation and parametric bootstrap recover the true number of clusters (four) in more than 90% of cases. The clusters were separated by three SPRs, and each locus had 40% mean taxon occupancy, which corresponds to the point on panel (A) indicated by the gray arrow.

Fig. 6.

Phylogenetic trees inferred from the three clusters found in the yeast analysis with treeCl. The tree on the left is that inferred from the largest cluster of 307 loci. This matches the established species tree for these 18 species of yeast. The taxa highlighted in red (Saccharomyces kudriavzevii) and blue (Saccharomyces kluyveri) are those that are found on long branches in the trees inferred from clusters 2 and 3 (shown respectively right, upper, and right, lower). In these trees, the branches leading to S. kudriavzevii (in cluster 2) and S. kluyveri (in cluster 3) have been truncated so as to fit reasonably on the plot. Their full lengths are as indicated. Otherwise, branch lengths can be determined by the scale bars shown (all equal scales). Branch support measures were calculated using approximate Bayes (aBayes). Where aBayes branch supports are less than the maximum possible value of 100%, their values are indicated by a number to the right of the branch.

Fig. 7.

Visualization of application of treeCl to the yeast data set. The scatterplot shows the embedding, by MDS, of the geodesic distances between the 344 trees. Three clusters were found by spectral clustering: red circles indicate the largest cluster, with 307 members; the 37 remaining loci are indicated by blue triangles (cluster 2) and green squares (cluster 3). Loci belonging to the first, largest cluster are tightly grouped and yield the correct species phylogeny, whereas trees belonging to the second and third clusters are disparate and all have odd and inconsistent phylogenies as a result of incorrectly called orthology (see text for full details).

Fig. 8.

Likelihood improvement gained when partitioning the Chiastocheta data into increasing numbers of clusters (red points). Resampled distributions (boxplots) were generated using the permutation procedure. The number of clusters selected by the stopping criterion is indicated by the vertical dashed line. For two to eight clusters, the improvement is statistically significant; increasing to nine clusters is not.

Fig. 9.

Trees obtained when clustering RAD-seq data from globeflower flies of the genus Chiastocheta. The trees are drawn to scale, and are rooted at their midpoint, as the outgroup is unknown. Leaves are colored according to species membership. Branch support is indicated as follows: branches with support values below 0.9 are collapsed into multifurcations; those with support in the range 0.9–0.95 are colored gray; those with support >0.95 are colored black. Support values are calculated using approximate Bayes (Anisimova et al. 2011).