Building functional networks of spiking model neurons
- PMID: 26906501
- PMCID: PMC4928643
- DOI: 10.1038/nn.4241
Building functional networks of spiking model neurons
Abstract
Most of the networks used by computer scientists and many of those studied by modelers in neuroscience represent unit activities as continuous variables. Neurons, however, communicate primarily through discontinuous spiking. We review methods for transferring our ability to construct interesting networks that perform relevant tasks from the artificial continuous domain to more realistic spiking network models. These methods raise a number of issues that warrant further theoretical and experimental study.
Conflict of interest statement
The authors declare no competing financial interests.
Figures
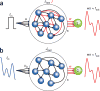

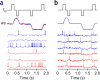
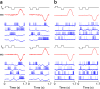
References
-
- Hansel D, Sompolinsky H. Modeling feature selectivity in local cortical circuits. In: Koch C, Segev I, editors. Methods in Neuronal Modeling. 2nd. MIT Press; Cambridge, Massachusetts, USA: 1998. pp. 499–566.
-
- Seung HS, Lee DD, Reis BY, Tank DW. Stability of the memory of eye position in a recurrent network of conductance-based model neurons. Neuron. 2000;26:259–271. - PubMed
-
- Wang XJ. Probabilistic decision making by slow reverberation in cortical circuits. Neuron. 2002;36:955–968. - PubMed
-
- Renart A, Song P, Wang XJ. Robust spatial working memory through homeostatic synaptic scaling in heterogeneous cortical networks. Neuron. 2003;38:473–485. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

