Stimuli Reduce the Dimensionality of Cortical Activity

Abstract

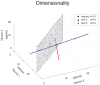
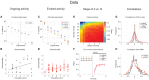
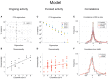
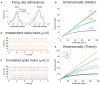
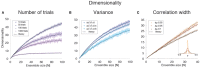
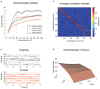
The activity of ensembles of simultaneously recorded neurons can be represented as a set of points in the space of firing rates. Even though the dimension of this space is equal to the ensemble size, neural activity can be effectively localized on smaller subspaces. The dimensionality of the neural space is an important determinant of the computational tasks supported by the neural activity. Here, we investigate the dimensionality of neural ensembles from the sensory cortex of alert rats during periods of ongoing (inter-trial) and stimulus-evoked activity. We find that dimensionality grows linearly with ensemble size, and grows significantly faster during ongoing activity compared to evoked activity. We explain these results using a spiking network model based on a clustered architecture. The model captures the difference in growth rate between ongoing and evoked activity and predicts a characteristic scaling with ensemble size that could be tested in high-density multi-electrode recordings. Moreover, we present a simple theory that predicts the existence of an upper bound on dimensionality. This upper bound is inversely proportional to the amount of pair-wise correlations and, compared to a homogeneous network without clusters, it is larger by a factor equal to the number of clusters. The empirical estimation of such bounds depends on the number and duration of trials and is well predicted by the theory. Together, these results provide a framework to analyze neural dimensionality in alert animals, its behavior under stimulus presentation, and its theoretical dependence on ensemble size, number of clusters, and correlations in spiking network models.

Keywords: dimensionality; gustatory cortex; hidden markov models; mean field theory; metastable dynamics; ongoing activity; spiking network model.

Figure 1

Dimensionality of the neural representation. Pictorial representation of the firing rate activity of an ensemble of N = 3 neurons. Each dot represents a three-dimensional vector of ensemble firing rates in one trial. Ensemble ongoing activity localizes around a plane (black dots cloud surrounding the shaded black plane), yielding a dimensionality of d = 1.8. Activity evoked by each of two different stimuli localizes around a line (red and blue dots clouds and lines), yielding a dimensionality of d = 0.9 in both cases.

Figure 2

Ensemble neural activity is characterized by sequences of states. (A) Upper panels: Representative trials from one ensemble of nine simultaneously recorded neurons during ongoing activity, segmented according to their ensemble states (HMM analysis, thin black vertical lines are action potentials; states are color-coded; smooth colored lines represent the probability for each state; shaded colored areas indicate intervals where the probability of a state exceeds 80%). Lower panels: Average firing rates across simultaneously recorded neurons (states are color-coded as in the upper panels). In total, 6 hidden states were found in this example session (only 5 states shown). X-axis for population rasters: time preceding the next event at (0 = stimulus delivery); Y-axis for population rasters: left, ensemble neuron index, right, probability of HMM states; X-axis for average firing rates panels: firing rates (spks/s); Y-axis for firing rate panels: ensemble neuron index. (B) Ensemble rasters and firing rates during evoked activity for four different tastes delivered at t = 0: sucrose, sodium chloride, citric acid, and quinine (notations as in panel A). In total, eight hidden states were found in this session during evoked activity.

Figure 3

Dependence of dimensionality on ensemble size (data). (A) Fraction of variance explained by each principal eigenvalue for an ensemble of 8 neurons during ongoing activity (corresponding to the filled dot in panel B) in the empirical dataset. The dashed vertical line represents the value of the dimensionality for this ensemble (d = 4.4). X-axis, eigenvalue number; Y-axis, fraction of variance explained by each eigenvalue. (B) Dimensionality of neural activity across all ensembles in the empirical dataset during ongoing activity (circles, linear regression fit, d = b · N + a, b = 0.26 ± 0.12, a = 1.07 ± 0.74, r = 0.4), estimated from HMM firing rate fits on all ongoing trials in each session (varying from 73 to 129). X-axis: ensemble size; Y-axis: dimensionality. (C) Fraction of variance explained by each principal eigenvalue for the ensemble in (A) during evoked activity. Principal eigenvalues for sucrose (S, orange), sodium chloride (N, yellow), citric acid (C, cyan), and quinine (Q, blue) are presented (corresponding to the color-coded dots in panel D). X-axis, eigenvalue number; Y-axis, percentage of variance explained by each eigenvalue. (D) Dimensionality of neural activity across all ensembles in the empirical dataset during evoked activity (notations as in panel B, linear regression: d = b · N + a, b = 0.13 ± 0.03, a = 1.27 ± 0.19, r = 0.39), estimated from HMM firing rate fits on evoked trials in each condition (varying from 7 to 11 trials across sessions for each tastant). (E) The slope of the linear regression of dimensionality (d) vs. ensemble size (N) as a function of the length of the trial interval and the number of trials used to estimate the dimensionality. X-axis, length of trial interval [s]; Y-axis, number of trials. (F) Time course of the trial-matched slopes of d vs. N, evaluated with 200 ms bins in consecutive 1 s intervals during ongoing (black curve, t < 0) and evoked periods (red curve, t > 0; error bars represent SD). A significant time course is triggered by stimulus presentation (see Results for details). The slopes of the empirical dataset (thick curves) were smaller than the slope of the shuffled dataset (dashed curves) during ongoing activity. X-axis, time from stimulus onset at t = 0 [s]; Y-axis, slope of d vs. N. (G) Distribution of pair-wise correlations in simultaneously recorded ensembles (black and red histograms for ongoing and evoked activity, respectively) and shuffled ensembles (brown and pink dashed histograms for ongoing and evoked activity, respectively) from 200 ms bins. X-axis, correlation; Y-axis, frequency. (H) Distribution of pair-wise correlations from HMM states during ongoing (black) and evoked activity (red) for all simultaneously recorded pairs of neurons. X-axis, correlation; Y-axis, frequency.

Figure 4

Recurrent network model. (A) Schematic recurrent network architecture. Triangles and squares represent excitatory and inhibitory LIF neurons respectively. Darker disks indicate excitatory clusters with potentiated intra-cluster synaptic weights. (B) Mean field solution of the recurrent network. Firing rates of the stable states for each subpopulation are shown as function of the intra-cluster synaptic potentiation parameter J₊: firing rate activity in the active clusters (solid gray lines), firing rate in the inactive clusters (dashed gray lines), activity of the background excitatory population (dashed blue lines), activity of the inhibitory population (solid red lines). In each case, darker colors represent configurations with larger number of active clusters. Numbers denote how many clusters are active in each stable configuration. Configurations with 1–8 active clusters are stable in the limit of infinite network size. A global configuration where all clusters are inactive (brown line) becomes unstable at the value J₊ = 5.15. The vertical green line represents the value of J₊ = 5.3 chosen for the simulations. X-axis, intra-cluster potentiation parameter J₊ in units of J_EE; Y-axis, Firing rate (spks/s).

Figure 5

Ensemble activity in the recurrent network model is characterized by sequences of states. Representative trials from one ensemble of nine simultaneously recorded neurons sampled from the recurrent network, segmented according to their ensemble states (notations as in Figure 1). (A) ongoing activity. (B) Ensemble activity evoked by four different stimuli, modeled as an increase in the external current to stimulus-selective clusters (see Methods for details).

Figure 6

Dependence of dimensionality on ensemble size (model). (A) Fraction of variance explained by each principal eigenvalue for an ensemble of 9 neurons during ongoing activity (corresponding to the filled dot in panel B) in the model network of Figure 5 (notations as in Figure 3A). (B) Dimensionality of neural activity across all ensembles in the model during ongoing activity (linear regression fit, d = b · N + a, b = 0.36 ± 0.07, a = 0.80 ± 0.43, r = 0.77), estimated from HMM firing rate fits. X-axis, ensemble size; Y-axis, dimensionality. (C) Fraction of variance explained by each principal eigenvalue for the ensemble in panel A during evoked activity. Principal eigenvalues for four tastes are presented (corresponding to the color-coded dots in panel D). X-axis, eigenvalue number; Y-axis, percentage of variance explained by each eigenvalue. (D) Dimensionality of neural activity across all ensembles in the model during evoked activity (notations as in panel B, linear regression: d = b · N + a, b = 0.12 ± 0.04, a = 1.70 ± 0.26, r = 0.29). (E) Distribution of pair-wise correlations in simultaneously recorded ensembles from the clustered network model (black and red histograms for ongoing and evoked activity, respectively) and in shuffled ensembles (brown and pink dashed histograms for ongoing and evoked activity, respectively) from 200 ms bins. X-axis, correlation; Y-axis, frequency. (F) Distribution of pair-wise correlations from HMM states during ongoing (black) and evoked activity (red) for all simultaneously recorded pairs of neurons. X-axis, correlation; Y-axis, frequency.

Figure 7

Dimensionality and correlation. (A) Empirical single neuron firing rate distributions in the data (left) and in the model (right), for ongoing (black), and evoked activity (red). The distributions are approximately lognormal. X-axis, Firing rate (spks/s); Y-axis, frequency. (B) Example of independent Poisson spike trains with firing rates matched to the firing rates obtained in simulations of the spiking network model. (C) Example of correlated Poisson spike trains with firing rates matched to the firing rates obtained in simulations of the spiking network model. Pair-wise correlations of ρ = 0.1 were used (see Methods). X-axis, time [s]; Y-axis, neuron index. (D) Dimensionality as a function of ensemble size N in an ensemble of Poisson spike trains with spike count correlations ρ = 0, 0.1, 0.2 and firing rates matched to the model simulations of Figure 6. Dashed lines represent the fit of Equation (16) to the data (with δρ² = αρ², σ⁴ = δσ⁴ = β), with best-fit parameters (mean ± s.e.m.) α = 0.22 ± 10⁻⁵, β = 340 ± 8. Filled circles (from top to bottom): dimensionality of the data (raster plots) shown in (B,C) (shaded areas represent SD). X-axis, ensemble size; Y-axis, dimensionality. (E) Theoretical prediction for the dependence of dimensionality on ensemble size N and firing rate correlation ρ for the case of uniform correlation, Equation (8) (thick lines; green to cyan to blue shades represent increasing correlations). “+” are dimensionality estimates from N_T = 1, 000 trials for each N (same N_T as in panel D, each trial providing a firing rate value sampled from a log-normal distribution), in the case of log-normally distributed firing rate variances ${\sigma }_i^2$ with mean σ² = 40 (spk∕s)^∧2 and standard deviation 0.5 σ². Theoretical predictions from Equation (16) match the estimated values in all cases (dashed black lines). X-axis, ensemble size N; Y-axis, dimensionality.

Figure 8

Dimensionality estimation. (A) Dependence of dimensionality on the number of trials for variable ensemble size N, for fixed correlations ρ = 0.1 and firing rates variances ${\sigma }_i^2$ with mean σ² and standard deviation δσ² = 0.4 σ². Dashed lines: theoretical prediction, Equation (16); dots: mean values from simulations of 20 surrogate datasets containing 10–1000 trials each (shaded areas: SD), with darker shades representing increasing number of trials. X-axis: ensemble size; Y-axis, dimensionality. (B) Dependence of dimensionality on the spread δσ² of the firing rates variances for fixed correlations ρ = 0.1 and firing rate variance with mean σ². Dashed lines: theoretical prediction, Equation (16); dots: mean values from simulations of 20 surrogate datasets containing 1000 trial each (shaded areas: SD), with lighter shades representing increasing values of δσ² ∕ σ²). X-axis, ensemble size; Y-axis, dimensionality. (C) Dependence of dimensionality on the width $\delta \rho =\sqrt{Var(\rho )}$ of pair-wise firing rate correlations (with zero mean, ρ = 0), for firing rates variances ${\sigma }_i^2$ with mean σ² and standard deviation δσ² = 0.4 σ². Dashed lines: theoretical prediction, Equation (16); dots: mean values from simulations of 20 surrogate datasets containing 1000 trials each (shaded areas: SD), with darker shades representing increasing values of δρ. Inset: distribution of correlation coefficients used in the main figure. X-axis, ensemble size; Y-axis, dimensionality. In all panels, σ² = 40 (spk∕s)^∧2.

Figure 9

Dimensionality in a clustered network. (A) Trial-matched dimensionality as a function of ensemble size in the recurrent network model (ongoing and evoked activity in black and red, respectively, with shaded areas representing s.e.m.). Filled lines represent ordered sampling, where ensembles to the left of the green vertical line (N = Q = 30) contain at most one neuron per cluster, while to the right of the line they contain one or more neurons from all clusters (filled circles indicate representative trials in panel B). Dashed lines represent random sampling of neurons, regardless of cluster membership. X-axis, ensemble size; Y-axis, dimensionality. (B) Representative trial of an ensemble of 50 neurons sampled from the recurrent network in Figure 4 during ongoing activity (upper plot, in black) or evoked activity (lower plot, in red) for the case of “ordered sampling” (full lines in panel A). Neurons are sorted according to their cluster membership (adjacent neuron pairs with similar activity belong to the same cluster, for neurons #1 up to #40; the last 10 neurons are sampled from the remaining clusters). X-axis, time to stimulus presentation at t = 0 (s); Y-axis, neuron index. (C) Average correlation matrix for 20 ensembles of N = 50 neurons from the clustered network model with Q = 30 clusters. For the first 40 neurons, adjacent pairs belong to the same cluster; the last 10 neurons (delimited by a dashed white square) belong to the remaining clusters (neurons are ordered as in panel B). Thus, neurons 1, 3, 5, …, 39 (20 neurons) belong to the first 20 clusters; neurons 2, 4, 6, …, 40 (20 neurons) belong also the first 20 clusters; and neurons 41, 42, 43, …, 50 (10 neurons) belong to the remaining 10 clusters. X-axis, Y-axis: neuron index. (D) Plot of Equation (12) giving d vs. N and ρ (uniform within-cluster correlations) for the sampling procedure of panel (B). X-axis, ensemble size N; Y-axis, dimensionality.