Inferring Population Size History from Large Samples of Genome-Wide Molecular Data - An Approximate Bayesian Computation Approach

Abstract

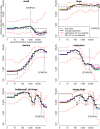
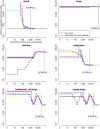
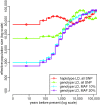
Inferring the ancestral dynamics of effective population size is a long-standing question in population genetics, which can now be tackled much more accurately thanks to the massive genomic data available in many species. Several promising methods that take advantage of whole-genome sequences have been recently developed in this context. However, they can only be applied to rather small samples, which limits their ability to estimate recent population size history. Besides, they can be very sensitive to sequencing or phasing errors. Here we introduce a new approximate Bayesian computation approach named PopSizeABC that allows estimating the evolution of the effective population size through time, using a large sample of complete genomes. This sample is summarized using the folded allele frequency spectrum and the average zygotic linkage disequilibrium at different bins of physical distance, two classes of statistics that are widely used in population genetics and can be easily computed from unphased and unpolarized SNP data. Our approach provides accurate estimations of past population sizes, from the very first generations before present back to the expected time to the most recent common ancestor of the sample, as shown by simulations under a wide range of demographic scenarios. When applied to samples of 15 or 25 complete genomes in four cattle breeds (Angus, Fleckvieh, Holstein and Jersey), PopSizeABC revealed a series of population declines, related to historical events such as domestication or modern breed creation. We further highlight that our approach is robust to sequencing errors, provided summary statistics are computed from SNPs with common alleles.

Fig 1. Optimization of ABC procedure.

Prediction error (left panel) and bias (right panel) for the estimated population size in each time window, evaluated from 2,000 random population size histories (see Methods). Summary statistics considered in the ABC analysis were (i) the AFS and (ii) the average zygotic LD for several distance bins. These statistics were computed from n = 25 diploid individuals, using all SNPs for AFS statistics and SNPs with a MAF above 20% for LD statistics. The posterior distribution of each parameter was obtained by rejection, ridge regression [33] or neural network regression [32]. The tolerance rate used for each of these approaches was the one providing the lowest prediction errors, for different values from 0.001 to 0.05. Population size point estimates were obtained from the median or the mode of the posterior distribution. The prediction errors were scaled in order that point estimates obtained from the prior distribution would result in a prediction error of 1.

Fig 2. Accuracy of ABC estimation and relative importance of the summary statistics.

Prediction error for the estimated population size in each time window (left) and standard deviation of this error (right), evaluated from 2,000 random population size histories. Summary statistics considered in the ABC analysis included different combinations of (i) the AFS (possibly without the overall proportion of SNPs) and (ii) the average zygotic LD for several distance bins. These statistics were computed from n = 25 diploid individuals, using all SNPs for AFS statistics and only those with a MAF above 20% for LD statistics. The posterior distribution of each parameter was obtained by neural network regression [32], with a tolerance rate of 0.005. Population size point estimates correspond to the median of the posterior distribution. The prediction errors were scaled in order that point estimates obtained from the prior distribution would result in a prediction error of 1.

Fig 3. Estimation of population size history using ABC in six different simulated scenarios.

a small constant population size (N = 500, top left), a large constant population size (N = 50,000, top right), a decline scenario mimicking the population size history in Holstein cattle (middle left), an expansion scenario mimicking the population size history in CEU human (middle right), a scenario with one expansion followed by one bottleneck (bottom left) and a zigzag scenario similar to that used in [10] (bottom right), with one expansion followed by two bottlenecks. For each scenario, the true population size history is shown by the dotted black line, the average estimated history over 20 PODs is shown by the solid black line, the estimated histories for five random PODs are shown by solid colored lines, and the 90% credible interval for one of these PODs is shown by the dotted red lines. The expected time to the most recent common ancestor (TMRCA) of the sample, E[TMRCA], is indicated by the vertical dotted black line. Summary statistics considered in the ABC analysis were (i) the AFS and (ii) the average zygotic LD for several distance bins. These statistics were computed from n = 25 diploid individuals, using all SNPs for AFS statistics and SNPs with a MAF above 20% for LD statistics. The posterior distribution of each parameter was obtained by neural network regression [32], with a tolerance rate of 0.005. Population size point estimates were obtained from the median of the posterior distribution.

Fig 4. Estimation of population size history using MSMC with two haplotypes in five different simulated scenarios.

For each scenario, the five PODs considered for MSMC estimation were the same as in Fig 3. The expected TMRCA shown here is also the same as in Fig 3, it corresponds to samples of 50 haploid sequences.

Fig 5. Influence of phasing and sequencing errors on ABC estimation.

Estimation of population size history in the Holstein cattle breed using ABC, based on whole genome NGS data from n = 25 animals. Summary statistics considered in the ABC analysis were (i) the AFS and (ii) the average LD for several distance bins. LD statistics were computed either from haplotypes or from genotypes, using SNPs with a MAF above 20%. AFS statistics were computed using either all SNPs or SNPs with a MAF above 10 or 20%. The posterior distribution of each parameter was obtained by neural network regression [32], with a tolerance rate of 0.005. Population size point estimates were obtained from the median of the posterior distribution. Generation time was assumed to be five years.

Fig 6. Estimation of population size history in four cattle breeds using ABC.

Angus (n = 25 animals), Fleckvieh (n = 25), Holstein (n = 25) and Jersey (n = 15). Estimations were obtained independently in each breed, based on whole genome NGS data from sampled animals. Summary statistics considered in the ABC analysis were (i) the AFS and (ii) the average zygotic LD for several distance bins. These statistics were computed using SNPs with a MAF above 20%. Other parameter settings are the same as in Fig 5.

Fig 7. Comparison of summary statistics for the estimation of population size history in three scenarios.

“bottleneck1 recent small” (top), “bottleneck cattle middle age” (middle) and “zigzag small” (bottom). Summary statistics considered in the ABC analysis were either the AFS statistics alone (left column), the LD statistics alone (middle column), or the AFS and LD statistics together (right column). All other settings are similar to Fig 3, as well as the legend.