Diffusion Decision Model: Current Issues and History
- PMID: 26952739
- PMCID: PMC4928591
- DOI: 10.1016/j.tics.2016.01.007
Diffusion Decision Model: Current Issues and History
Abstract
There is growing interest in diffusion models to represent the cognitive and neural processes of speeded decision making. Sequential-sampling models like the diffusion model have a long history in psychology. They view decision making as a process of noisy accumulation of evidence from a stimulus. The standard model assumes that evidence accumulates at a constant rate during the second or two it takes to make a decision. This process can be linked to the behaviors of populations of neurons and to theories of optimality. Diffusion models have been used successfully in a range of cognitive tasks and as psychometric tools in clinical research to examine individual differences. In this review, we relate the models to both earlier and more recent research in psychology.
Keywords: diffusion model; nonstationarity; optimality; response time.
Copyright © 2016. Published by Elsevier Ltd.
Figures

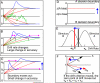
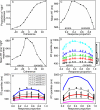


References
-
- Ratcliff R. A theory of memory retrieval. Psychol. Rev. 1978;85:59–108.
-
- Ratcliff R. A theory of order relations in perceptual matching. Psychol. Rev. 1981;88:552–572.
-
- Ratcliff R, Rouder JN. Modeling response times for two-choice decisions. Psychol. Sci. 1998;9:347–356.
-
- Ratcliff R, et al. Connectionist and diffusion models of reaction time. Psychol. Rev. 1999;106:261–300. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

