Extracting a shape function for a signal with intra-wave frequency modulation

Abstract

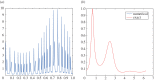
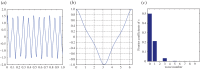
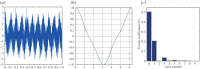
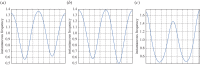
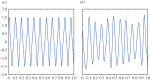
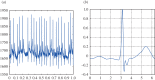
In this paper, we develop an effective and robust adaptive time-frequency analysis method for signals with intra-wave frequency modulation. To handle this kind of signals effectively, we generalize our data-driven time-frequency analysis by using a shape function to describe the intra-wave frequency modulation. The idea of using a shape function in time-frequency analysis was first proposed by Wu (Wu 2013 Appl. Comput. Harmon. Anal. 35, 181-199. (doi:10.1016/j.acha.2012.08.008)). A shape function could be any smooth 2π-periodic function. Based on this model, we propose to solve an optimization problem to extract the shape function. By exploring the fact that the shape function is a periodic function with respect to its phase function, we can identify certain low-rank structure of the signal. This low-rank structure enables us to extract the shape function from the signal. Once the shape function is obtained, the instantaneous frequency with intra-wave modulation can be recovered from the shape function. We demonstrate the robustness and efficiency of our method by applying it to several synthetic and real signals. One important observation is that this approach is very stable to noise perturbation. By using the shape function approach, we can capture the intra-wave frequency modulation very well even for noise-polluted signals. In comparison, existing methods such as empirical mode decomposition/ensemble empirical mode decomposition seem to have difficulty in capturing the intra-wave modulation when the signal is polluted by noise.

Keywords: intra-wave frequency modulation; shape function; sparse time-frequency decomposition.

Figure 1.

One example of signals with intra-wave modulation: Stokes wave. (Adapted from [3].)

Figure 2.

(a) The original datain example 5.1. (b) The shape function obtained by our method (blue) and the exact shape function (red). (Online version in colour.)

Figure 3.

(a)The noise data f(t)+0.3X(t), where f(t) is given in example 5.1 and X(t) is the white noise with standard derivative σ²=1. (b) The shape function obtained by our method (blue) and the exact shape function (red). (Online version in colour.)

Figure 4.

(a) The solution of the Duffing equation; (b) the shape function s; (c) the Fourier coefficients of s. (Online version in colour.)

Figure 5.

(a) The solution of the Duffing equation with noise X(t); (b) the shape function s; and (c) the Fourier coefficients of s. (Online version in colour.)

Figure 6.

(a) The instantaneous frequency recovered from the shape function for the solution of the Duffing equation; (b) the instantaneous frequency recovered from the shape function for the solution of the Duffing equation with noise; and (c) the instantaneous frequency given by the EMD for the noise-free solution in one wave cycle. (Online version in colour.)

Figure 7.

The IMFs given by the EMD/EEMD in the noise-free case (a) and the noisy case (b). (Online version in colour.)

Figure 8.

(a) The original electrocardiogram (ECG) data and (b) the shape function obtained by our method for the ECG data. (Online version in colour.)