Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
Review
. 2016 Apr 13;374(2065):20150203.
doi: 10.1098/rsta.2015.0203.

Understanding deep convolutional networks

Stéphane Mallat  1
Affiliations
Review

Understanding deep convolutional networks

Stéphane Mallat. Philos Trans A Math Phys Eng Sci. .

Abstract

Deep convolutional networks provide state-of-the-art classifications and regressions results over many high-dimensional problems. We review their architecture, which scatters data with a cascade of linear filter weights and nonlinearities. A mathematical framework is introduced to analyse their properties. Computations of invariants involve multiscale contractions with wavelets, the linearization of hierarchical symmetries and sparse separations. Applications are discussed.

Keywords: deep convolutional neural networks; learning; wavelets.

PubMed Disclaimer

Figures

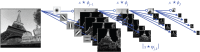
Figure 1.
Figure 1.
Wavelet transform of an image x(u), computed with a cascade of convolutions with filters over J=4 scales and K=4 orientations. The low-pass and K=4 band-pass filters are shown on the first arrows. (Online version in colour.)
Figure 2.
Figure 2.
A convolution network iteratively computes each layer xj by transforming the previous layer xj−1, with a linear operator Wj and a pointwise nonlinearity ρ. (Online version in colour.)
Figure 3.
Figure 3.
First row: original images. Second row: realization of a Gaussian process with same second covariance moments. Third row: reconstructions from first- and second-order scattering coefficients.
Figure 4.
Figure 4.
A multiscale hierarchical networks computes convolutions along the fibres of a parallel transport. It is defined by a group Gj of symmetries acting on the index set Pj of a layer xj. Filter weights are transported along fibres. (Online version in colour.)
See this image and copyright information in PMC

References

    1. Le Cun Y, Bengio Y, Hinton G. 2015. Deep learning. Nature 521, 436–444. (10.1038/nature14539) - DOI - PubMed
    1. Krizhevsky A, Sutskever I, Hinton G. 2012. ImageNet classification with deep convolutional neural networks. In Proc. 26th Annual Conf. on Neural Information Processing Systems, Lake Tahoe, NV, 3–6 December 2012, pp. 1090–1098.
    1. Hinton G. et al. 2012. Deep neural networks for acoustic modeling in speech recognition. IEEE Signal Process. Mag. 29, 82–97. (10.1109/MSP.2012.2205597) - DOI
    1. Leung MK, Xiong HY, Lee LJ, Frey BJ. 2014. Deep learning of the tissue regulated splicing code. Bioinformatics 30, i121–i129. (10.1093/bioinformatics/btu277) - DOI - PMC - PubMed
    1. Sutskever I, Vinyals O, Le QV. 2014. Sequence to sequence learning with neural networks. In Proc. 28th Annual Conf. on Neural Information Processing Systems, Montreal, Canada, 8–13 December 2014.

Publication types