Mixed-mode oscillations and population bursting in the pre-Bötzinger complex
- PMID: 26974345
- PMCID: PMC4846382
- DOI: 10.7554/eLife.13403
Mixed-mode oscillations and population bursting in the pre-Bötzinger complex
Abstract
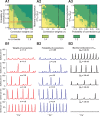
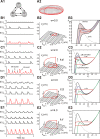
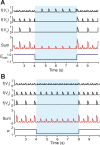
This study focuses on computational and theoretical investigations of neuronal activity arising in the pre-Bötzinger complex (pre-BötC), a medullary region generating the inspiratory phase of breathing in mammals. A progressive increase of neuronal excitability in medullary slices containing the pre-BötC produces mixed-mode oscillations (MMOs) characterized by large amplitude population bursts alternating with a series of small amplitude bursts. Using two different computational models, we demonstrate that MMOs emerge within a heterogeneous excitatory neural network because of progressive neuronal recruitment and synchronization. The MMO pattern depends on the distributed neuronal excitability, the density and weights of network interconnections, and the cellular properties underlying endogenous bursting. Critically, the latter should provide a reduction of spiking frequency within neuronal bursts with increasing burst frequency and a dependence of the after-burst recovery period on burst amplitude. Our study highlights a novel mechanism by which heterogeneity naturally leads to complex dynamics in rhythmic neuronal populations.
Keywords: central pattern generator; computational biology; computational modeling; mixed-mode oscillations; neural oscillations; neuroscience; none; pre-Bӧtzinger complex; respiration; systems biology.
Conflict of interest statement
The authors declare that no competing interests exist.
Figures




References
-
- Ben-Mabrouk F, Amos LB, Tryba AK. Metabotropic glutamate receptors (mGluR5) activate transient receptor potential canonical channels to improve the regularity of the respiratory rhythm generated by the pre-Bötzinger complex in mice. European Journal of Neuroscience. 2012;35:1725–1737. doi: 10.1111/j.1460-9568.2012.08091.x. - DOI - PMC - PubMed
-
- Butera RJ, Rinzel J, Smith JC. Models of respiratory rhythm generation in the pre-Bötzinger complex. I. Bursting pacemaker neurons. Journal of Neurophysiology. 1999a;82:382–397. - PubMed
-
- Butera RJ, Rinzel J, Smith JC. Models of respiratory rhythm generation in the pre-Bötzinger complex. II. Populations Of coupled pacemaker neurons. Journal of Neurophysiology. 1999b;82:398–415. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

