Phase transitions in semidefinite relaxations
- PMID: 27001856
- PMCID: PMC4843421
- DOI: 10.1073/pnas.1523097113
Phase transitions in semidefinite relaxations
Abstract
Statistical inference problems arising within signal processing, data mining, and machine learning naturally give rise to hard combinatorial optimization problems. These problems become intractable when the dimensionality of the data is large, as is often the case for modern datasets. A popular idea is to construct convex relaxations of these combinatorial problems, which can be solved efficiently for large-scale datasets. Semidefinite programming (SDP) relaxations are among the most powerful methods in this family and are surprisingly well suited for a broad range of problems where data take the form of matrices or graphs. It has been observed several times that when the statistical noise is small enough, SDP relaxations correctly detect the underlying combinatorial structures. In this paper we develop asymptotic predictions for several detection thresholds, as well as for the estimation error above these thresholds. We study some classical SDP relaxations for statistical problems motivated by graph synchronization and community detection in networks. We map these optimization problems to statistical mechanics models with vector spins and use nonrigorous techniques from statistical mechanics to characterize the corresponding phase transitions. Our results clarify the effectiveness of SDP relaxations in solving high-dimensional statistical problems.
Keywords: community detection; phase transitions; semidefinite programming; synchronization.
Conflict of interest statement
The authors declare no conflict of interest.
Figures
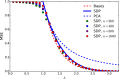
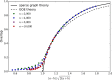
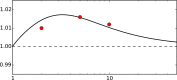
Comment in
-
Inference on graphs via semidefinite programming.Proc Natl Acad Sci U S A. 2016 Apr 19;113(16):4238-9. doi: 10.1073/pnas.1603405113. Epub 2016 Apr 8. Proc Natl Acad Sci U S A. 2016. PMID: 27071125 Free PMC article. No abstract available.
References
-
- Gauss CF. Theoria motus corporum coelestium in sectionibus conicis solem ambientium auctore Carolo Friderico Gauss. Friedrich Perthes und I. H. Besser; Hamburg, Germany: 1809.
-
- Ben-Dor A, Shamir R, Yakhini Z. Clustering gene expression patterns. J Comput Biol. 1999;6(3-4):281–297. - PubMed
-
- Plaza A, et al. Recent advances in techniques for hyperspectral image processing. Remote Sens Environ. 2009;113(1):S110–S122.
-
- Koren Y, Bell R, Volinsky C. Matrix factorization techniques for recommender systems. Computer. 2009;42(8):30–37.
-
- Von Luxburg U. A tutorial on spectral clustering. Stat Comput. 2007;17(4):395–416.
Publication types
LinkOut - more resources
Full Text Sources
Other Literature Sources

