An engineering viewpoint on biological robustness

Abstract

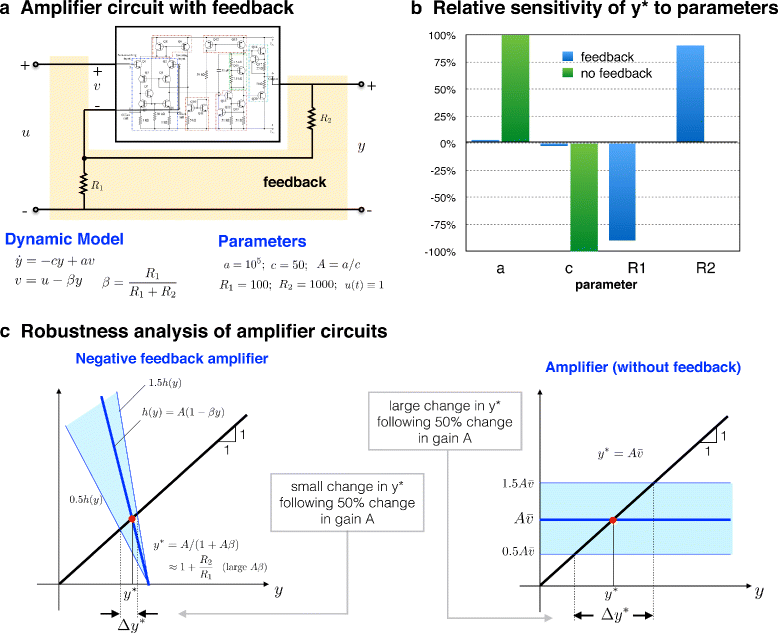
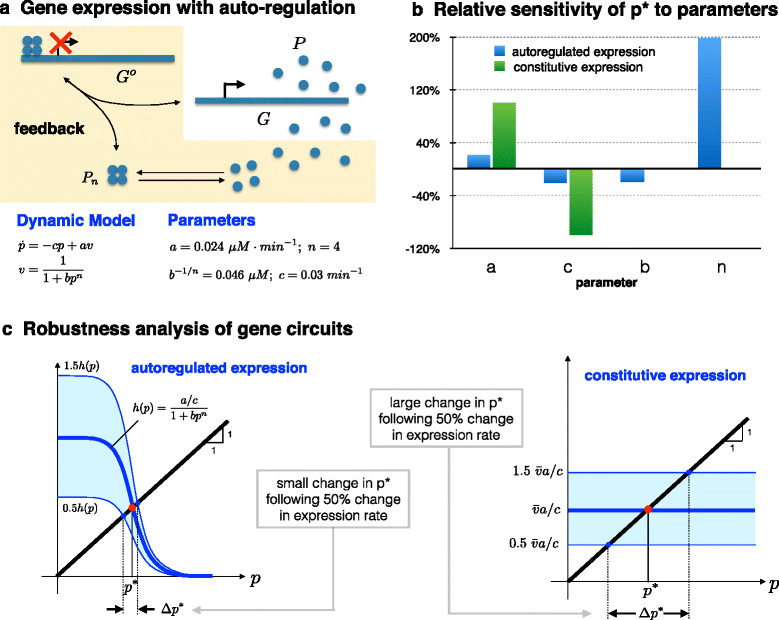
In his splendid article "Can a biologist fix a radio?--or, what I learned while studying apoptosis," Y. Lazebnik argues that when one uses the right tools, similarity between a biological system, like a signal transduction pathway, and an engineered system, like a radio, may not seem so superficial. Here I advance this idea by focusing on the notion of robustness as a unifying lens through which to view complexity in biological and engineered systems. I show that electronic amplifiers and gene expression circuits share remarkable similarities in their dynamics and robustness properties. I explore robustness features and limitations in biology and engineering and highlight the role of negative feedback in shaping both.

Fig. 1.

Robustness of two electronic operational amplifiers (with and without negative feedback). a A common model of a negative feedback amplifier with typical parameters. y is the output to input u(t), which I take to be unity. Shown also is the unregulated amplifier (circuit inside the rectangle) with input v and output y. This high gain amplifier is manufactured as an integrated transistor circuit. a and c are internal parameters such that c ⁻¹ is the time constant and A=a/c is the amplifier gain. Negative feedback is introduced by adding the two resistors R ₁ and R ₂ in the configuration shown. The circuit is quite complex, but the simple first order model shown is a good representation of its behavior under typical operating conditions. The feedback resistors R ₁ and R ₂ are supplied by the user and are selected to tune the gain. b The robustness/fragility properties of the two amplifier circuits. For proper comparison, the input to the unregulated amplifier, $v\left(t\right)\equiv \overline{v}$, is chosen so that the corresponding output y ^∗ matches that of the negative feedback amplifier. For the feedback amplifier, y ^∗ is extremely robust to variations in the parameters a and c, in contrast to the unregulated amplifier. At the same time, y ^∗ is quite sensitive to the values of the two resistors, underscoring its robust yet fragile character. c Graphical explanation of the difference in robustness properties of the two amplifiers. For both amplifiers, the abscissa of the point of intersection of the black line and the blue line gives y ^∗. In the case of the feedback amplifier, the slope of the blue line is −A β. As A β>>1, one can see that y ^∗ will be almost independent of A. Indeed, y ^∗ depends almost exclusively on the ratio R ₂/R ₁, resulting in extreme robustness to A=a/c

Fig. 2.

Robustness properties of two gene expression circuits (auto-regulated with negative feedback versus constitutively expressed without feedback). a The model of the auto-regulated gene expression circuit. Negative feedback is achieved by a Hill-type function resulting from the multimerization of the protein P into an n-mer P _n, which in turn binds to the active gene G and represses it. Constitutive expression is modeled by an expression rate av that is independent of p. b The relative sensitivities of p ^∗, the steady-state concentration of the protein, to the model parameters in both circuits. The auto-regulated circuit is robust to parameters a and c, in contrast to the constitutively expressed circuit, which is sensitive to both parameters. The auto-regulated gene circuit is, however, sensitive to parameter n. c A graphical explanation of the differences in robustness between both circuits. The intersection of the line and the graph of h(·) in the left figure (auto-regulated circuit) gives p ^∗. Robustness in this circuit is achieved through high-gain and feedback, just as it is in the amplifier circuit. The higher the gain n the more robust the value of p ^∗ will be to variations in the parameters a, c, and b. Indeed it can be shown that $S_a\left(\mathit{\theta }\right)\approx \frac{1}{n+1}$, $S_c\left(\mathit{\theta }\right)\approx \frac{-1}{n+1}$, $S_b\left(\mathit{\theta }\right)\approx \frac{-1}{n+1}$, and $S_n\left(\mathit{\theta }\right)\approx \frac{-nlog{p}^{\ast }}{n+1}$. In contrast, the constitutively expressed gene circuit lacks robustness to parameters a and c, even though it shares the same protein level p ^∗ as the auto-regulated circuit. See also [20] for a general discussion of sensitivity of biochemical reactions and the effect of feedback

Fig. 3.

Renewal control. a A stem cell (type 1) can either regenerate or differentiate into a terminal post-mitotic cell (type 2). Negative feedback acts to affect the probability of regeneration. b The effect of sinusoidal variation in d (the disturbance) on |S|, the so-called ‘sensitivity function’, as a function of disturbance frequency. |S| is in turn related to the size of the corresponding fluctuation of the population of terminal cells (type 2). n reflects the strength of feedback, with stronger feedback resulting in better disturbance rejection (better robustness) at lower frequencies, at the price of amplifying the effect of disturbances at mid-frequencies (fragility)

Fig. 4.

X-29 experimental aircraft. The forward-swept wings configuration of the X-29 makes the design of robust feedback control systems more difficult compared to more conventional aircraft. (Courtesy of NASA)

Fig. 5.

Fate control. a A stem cell (type 1) can either regenerate, or differentiate into a terminal post-mitotic cell (type 2), or have a third alternative fate that leads to a new branch. Negative feedback of the population of terminal cells acts on the probability of regeneration and differentiation, which necessarily leads to a positive feedback on the alternative fate as the three probabilities must sum to 1. b The effect of sinusoidal variation in d (the disturbance) on |S|, the ‘sensitivity function’, as a function of disturbance frequency. |S| is related to the size of the corresponding fluctuation of the population of terminal cells. n reflects the strength of feedback. For this fate control model p _r(x ₂) is the same as in the renewal control case, while p _d(x ₂) is taken to be p _r(x ₂)/2. As in renewal control, stronger feedback results in better disturbance rejection (better robustness) at lower frequencies, at the price of poor disturbances rejection at mid-frequencies. Unlike renewal control, however, the system has significantly more capacity for disturbance rejection (more overall robustness), as indicated by the much larger area below the gray line