Dynamic similarity promotes interpersonal coordination in joint action

Abstract

Human movement has been studied for decades, and dynamic laws of motion that are common to all humans have been derived. Yet, every individual moves differently from everyone else (faster/slower, harder/smoother, etc.). We propose here an index of such variability, namely an individual motor signature (IMS) able to capture the subtle differences in the way each of us moves. We show that the IMS of a person is time-invariant and that it significantly differs from those of other individuals. This allows us to quantify the dynamic similarity, a measure of rapport between dynamics of different individuals' movements, and demonstrate that it facilitates coordination during interaction. We use our measure to confirm a key prediction of the theory of similarity that coordination between two individuals performing a joint-action task is higher if their motions share similar dynamic features. Furthermore, we use a virtual avatar driven by an interactive cognitive architecture based on feedback control theory to explore the effects of different kinematic features of the avatar motion on coordination with human players.

Keywords: mathematical modelling; movement dynamics; statistical analysis.

Figure 1.

Individual motor signature in the similarity space computed with MDS from distances between velocity profiles. (a) For 15 different participants from solo mirror game recordings in scenario 1, on three different days with at least one week break between recording rounds. (b) For 56 solo trials of 14 participants from solo mirror game recordings in scenario 3 (for the sake of clarity data for only 14 of 51 participants is shown). Each ellipse corresponds to a different participant. Small dots correspond to individual solo recordings. Each cross at the centre of an ellipse corresponds to the average of the small dots' positions. Each ellipse indicates 0.7 mass of bivariate normal distribution fitted to the small dots (see the electronic supplementary material, §5 for further details).

Figure 2.

Interaction between two players in different experimental conditions visualized in the similarity space. Ellipses encircle points corresponding to velocity profiles in solo (S1 and S2; light grey), leader (L1 and L2; dark grey), follower (F1 and F2; dark grey) and joint improvisation (JI1 and JI2; dark grey) rounds. Each row depicts data for a different dyad. In column 1, player 1 was a leader, in column 2, player 2 was a leader and in column 3, participants played in joint improvisation condition. x-Axis has the same range in all panels, y-axis is rescaled for clarity of presentation.

Figure 3.

First, we compute dynamic similarity between two players. In panel (a(i)), we show the solo movements of two participants who later played together in the leader–follower condition. Panels (a(ii)) and (a(iii)) depict velocity profiles that represent individual motor signatures of the two players (S_a(ii), and S_a(iii)) corresponding to the positions timeseries presented in panel (a(i)). The EMD(S_a(ii), S_a(iii)) = 0.0303 between the histograms in panels (a(ii)) and (a(iii)) quantifies dynamic similarity between the two players. Then, we measure temporal correspondence between their movements when they play together in the leader–follower condition. Panel (b) illustrates position traces of the participants from panel (a) when they play together as a leader (black) and follower (grey). Panel (c) shows the RPE between leader and follower trajectories presented in panel (b). The mean value and the standard deviation of the RPE are respectively μRPE(L_a(ii), F_a(iii)) = 0.05 and σRPE(L_a(ii), F_a(iii)) = 0.05.

Figure 4.

Panel (a) shows correlation between EMD(S_L, S_F) and RPE(L, F) computed for all individual leader–follower trials in eight dyads from scenario 2. Panels (b) depicts the dependence of RPE(L_VP, F_H) between the VP leading the human participant on EMD(Ref, S_F) between the reference trajectory and the participant's solo movement (scenario 3). Each black dot corresponds to a single leader–follower trial. Grey lines are presented only for illustrative purposes. Spearman's ρ coefficients are equal to: ρ_a = 0.3907 (p_ρa = 7×10⁻³), ρ_b = 0.2224 (p_ρb<1 × 10⁻⁵); Pearson's R² coefficients are equal to:

Figure 5.

Panel (a) shows a velocity profile—histogram (h_a; black) of the velocity timeseries. Panel (b) shows histogram (h_b; grey) of a random variable generated with distribution of type 1 from the Pearson system. Both samples have μ=−0.01, σ = 0.54, s=−0.04 and k = 1.82, where μ is the mean, σ is the standard deviation, s is the skewness and k is the kurtosis. Panel (c) shows cumulative density functions of the distribution from panel (a) in black and from panel (b) in grey. The light grey shading indicates the area of difference between the CDFs, i.e. the EMD between the two distributions,

Figure 6.

(a) Similarity space shows points corresponding to velocity profiles of normalized solo data from the scenarios 1 (multiplication symbol) and 3 (bullets). Insets (a(i))–(a(viii)) show examples of the velocity profiles. v is velocity, t is time and T indicates normalized duration of the velocity segment. (b) Relation between y-coordinate of the similarity space and average kurtosis of the velocity segments: Corr(y, μ(kurtosis of vel. 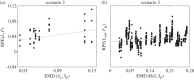segments)): R² = 0.5657 (), ρ = 0.5685 (p_ρ = 0). (c) Relation between x-coordinate of the similarity space and average solo velocity of a participant: Corr(x, μ|v|): R² = 0.9993 (), ρ = 0.9979 (p_ρ = 0).

Figure 7.

Illustration of the principle used for computing relative position error (RPE). In panels (a(i)) and (b(i)), the black lines indicate leader's position and the grey lines indicate follower's position. Grey arrows show direction of motion of the follower. At the times indicated by double grey-black arrows, the participants move in opposite directions. Panels (a(ii)) and (b(ii)) show corresponding RPE (black). Time runs from bottom to top.