Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2015 Dec 1;110(512):1479-1490.
doi: 10.1080/01621459.2014.960967. Epub 2014 Sep 25.

Dirichlet-Laplace priors for optimal shrinkage

Anirban Bhattacharya  1 , Debdeep Pati  1 , Natesh S Pillai  1 , David B Dunson  1
Affiliations

Dirichlet-Laplace priors for optimal shrinkage

Anirban Bhattacharya et al. J Am Stat Assoc. .

Abstract

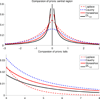
Penalized regression methods, such as L1 regularization, are routinely used in high-dimensional applications, and there is a rich literature on optimality properties under sparsity assumptions. In the Bayesian paradigm, sparsity is routinely induced through two-component mixture priors having a probability mass at zero, but such priors encounter daunting computational problems in high dimensions. This has motivated continuous shrinkage priors, which can be expressed as global-local scale mixtures of Gaussians, facilitating computation. In contrast to the frequentist literature, little is known about the properties of such priors and the convergence and concentration of the corresponding posterior distribution. In this article, we propose a new class of Dirichlet-Laplace priors, which possess optimal posterior concentration and lead to efficient posterior computation. Finite sample performance of Dirichlet-Laplace priors relative to alternatives is assessed in simulated and real data examples.

Keywords: Bayesian; Convergence rate; High dimensional; L1; Lasso; Penalized regression; Regularization; Shrinkage prior.

PubMed Disclaimer

Figures

Figure 1
Figure 1
Marginal density of the DL prior with a = 1/2 in comparison to other shrinkage priors.
Figure 2
Figure 2
Simulation results from a single replicate with n = 200, qn = 10, A = 7. Blue circles = entries of y, red circles = posterior median of θ, shaded region: 95% point wise credible interval for θ. Left panel: Bayesian lasso, right panel: DL1/n prior
Figure 3
Figure 3
Simulation results from a single replicate with n = 200, qn = 10, A = 7. Blue circles = entries of y, red circles = posterior median of θ, shaded region: 95% point wise credible interval for θ. Left panel: Horseshoe, right panel: DL1/2 prior
Figure 4
Figure 4
Histogram of z-values
See this image and copyright information in PMC

References

    1. Abramowitz M, Stegun IA. Handbook of mathematical functions: with formulas, graphs, and mathematical tables. Vol. 55. Dover publications; 1965.
    1. Alzer H. On some inequalities for the incomplete gamma function. Mathematics of Computation. 1997;66(218):771–778.
    1. Armagan A, Dunson D, Lee J. Generalized double pareto shrinkage. Statistica Sinica, to appear. 2013 - PMC - PubMed
    1. Armagan Artin, Dunson David B, Lee Jaeyong, Bajwa Waheed U, Strawn Nate. Posterior consistency in linear models under shrinkage priors. Biometrika. 2013;100(4):1011–1018.
    1. Benjamini Yoav, Hochberg Yosef. Controlling the false discovery rate: a practical and powerful approach to multiple testing. Journal of the Royal Statistical Society. Series B (Methodological) 1995:289–300.

LinkOut - more resources