Cross-validation and Peeling Strategies for Survival Bump Hunting using Recursive Peeling Methods
- PMID: 27034730
- PMCID: PMC4809437
- DOI: 10.1002/sam.11301
Cross-validation and Peeling Strategies for Survival Bump Hunting using Recursive Peeling Methods
Abstract
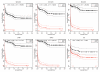
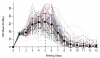
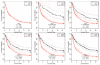
We introduce a framework to build a survival/risk bump hunting model with a censored time-to-event response. Our Survival Bump Hunting (SBH) method is based on a recursive peeling procedure that uses a specific survival peeling criterion derived from non/semi-parametric statistics such as the hazards-ratio, the log-rank test or the Nelson--Aalen estimator. To optimize the tuning parameter of the model and validate it, we introduce an objective function based on survival or prediction-error statistics, such as the log-rank test and the concordance error rate. We also describe two alternative cross-validation techniques adapted to the joint task of decision-rule making by recursive peeling and survival estimation. Numerical analyses show the importance of replicated cross-validation and the differences between criteria and techniques in both low and high-dimensional settings. Although several non-parametric survival models exist, none addresses the problem of directly identifying local extrema. We show how SBH efficiently estimates extreme survival/risk subgroups unlike other models. This provides an insight into the behavior of commonly used models and suggests alternatives to be adopted in practice. Finally, our SBH framework was applied to a clinical dataset. In it, we identified subsets of patients characterized by clinical and demographic covariates with a distinct extreme survival outcome, for which tailored medical interventions could be made. An R package PRIMsrc (Patient Rule Induction Method in Survival, Regression and Classification settings) is available on CRAN (Comprehensive R Archive Network) and GitHub.
Keywords: Bump Hunting; Cross-Validation; Exploratory Survival/Risk Analysis; Non-Parametric Method; Patient Rule-Induction Method; Survival/Risk Estimation & Prediction.
Figures
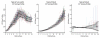






Similar articles
-
R package PRIMsrc: Bump Hunting by Patient Rule Induction Method for Survival, Regression and Classification.Proc Am Stat Assoc. 2015 Aug;2015:650-664. Proc Am Stat Assoc. 2015. PMID: 26798326 Free PMC article.
-
Cross-Validation of Survival Bump Hunting by Recursive Peeling Methods.Proc Am Stat Assoc. 2014 Aug;2014:3366-3380. Proc Am Stat Assoc. 2014. PMID: 26997922 Free PMC article.
-
Local Sparse Bump Hunting.J Comput Graph Stat. 2010 Dec;19(4):900-929. doi: 10.1198/jcgs.2010.09029. J Comput Graph Stat. 2010. PMID: 22399839 Free PMC article.
-
Avoiding and identifying errors in health technology assessment models: qualitative study and methodological review.Health Technol Assess. 2010 May;14(25):iii-iv, ix-xii, 1-107. doi: 10.3310/hta14250. Health Technol Assess. 2010. PMID: 20501062 Review.
-
Reviewing ensemble classification methods in breast cancer.Comput Methods Programs Biomed. 2019 Aug;177:89-112. doi: 10.1016/j.cmpb.2019.05.019. Epub 2019 May 20. Comput Methods Programs Biomed. 2019. PMID: 31319964 Review.
Cited by
-
R package PRIMsrc: Bump Hunting by Patient Rule Induction Method for Survival, Regression and Classification.Proc Am Stat Assoc. 2015 Aug;2015:650-664. Proc Am Stat Assoc. 2015. PMID: 26798326 Free PMC article.
References
-
- Hartigan J, Mohanty S. The runt test for multimodality. Joumal of Classification. 1992;9:63–70.
-
- Rozal G, Hartigan J. The map test for multimodality. Journal of Classification. 1994;11:5–36.
-
- Polonik W. Measuring mass concentration and estimating density contour clusters: an excess mass approach. The Annals of Statistics. 1995;23:855–881.
-
- Burman P, Polonik W. Multivariate mode hunting: Data analytic tools with measures of significance. Journal of Multivariate Analysis. 2009;100:1198–1218.
-
- Bhning D, Seidel W. Editorial: recent developments in mixture models. Comp. Stat. Data Anal. 2003;41(no. 34):349–357.
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
