Infections on Temporal Networks--A Matrix-Based Approach

Abstract

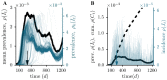
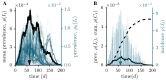
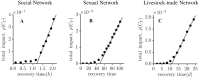
We extend the concept of accessibility in temporal networks to model infections with a finite infectious period such as the susceptible-infected-recovered (SIR) model. This approach is entirely based on elementary matrix operations and unifies the disease and network dynamics within one algebraic framework. We demonstrate the potential of this formalism for three examples of networks with high temporal resolution: networks of social contacts, sexual contacts, and livestock-trade. Our investigations provide a new methodological framework that can be used, for instance, to estimate the epidemic threshold, a quantity that determines disease parameters, for which a large-scale outbreak can be expected.

Fig 1. Transitivity is not assured in temporal networks.

Here, links 1 → 2 and 2 → 3 exist, but the temporal order (1 → 2 at time t = 1 and 2 → 3 at time t = 0) prevents information to spread from node 1 to 3.

Fig 2. Prevalence, incidence and cumulative incidence for the social contacts network.

(A) Comparison between the individual single source outbreaks (blue, right axes) and the corresponding, averaged prevalence (black, left axes). The infectious period is fixed at τ = 20h. The arrow at t = 14.8h indicates the maximum averaged prevalence. (B) Mean prevalence ρ(I_t) (solid curves), incidence ρ(J_t) (blue bars, right scale) and cumulative incidence ρ(C_t) (dashed curves). Here, the arrow points at the maximum averaged incidence (t = 1.8h).

Fig 3. Prevalence, incidence and cumulative incidence for the sexual contacts network.

(A) Comparison between the individual single source outbreaks (blue, right axes) and the corresponding, averaged prevalence (black, left axes). The infectious period is fixed at τ = 91 d. The arrow indicates the maximum averaged prevalence. (B) Mean prevalence ρ(I_t) (solid curves), incidence ρ(J_t) (blue bars, right scale) and cumulative incidence ρ(C_t) (dashed curves). Here, the arrow points at the maximum averaged incidence.

Fig 4. Prevalence, incidence and cumulative incidence for the livestock-trade network.

(A) Comparison between the individual single source outbreaks (blue, right axes) and the corresponding, averaged prevalence (black, left axes). The infectious period is fixed at τ = 14 d. The arrow indicates the maximum averaged prevalence. (B) Mean prevalence ρ(I_t) (solid curves), incidence ρ(J_t) (blue bars, right scale) and cumulative incidence ρ(C_t) (dashed curves). Here, the arrow points at the maximum averaged incidence.

Fig 5. Estimating the critical infectious period for the social (A), the sexual (B) and the livestock-trade network (C).

Fraction of nodes, which have been infected up to the observation time as a function of the infectious period τ. The grey line is a linear regression through the last 6 data points and the zero crossing gives a rough estimate of the critical infectious period τ_c. We found τ_c = 1.20 ± 0.05 hours, τ_c = 48 ± 2 days and τ_c = 10.8 ± 0.3 days for the social, the sexual and the livestock-trade network, respectively. The uncertainties are calculated from the least-squares fit.