Modeling and analysis of collective cell migration in an in vivo three-dimensional environment
- PMID: 27035964
- PMCID: PMC4839456
- DOI: 10.1073/pnas.1522656113
Modeling and analysis of collective cell migration in an in vivo three-dimensional environment
Abstract
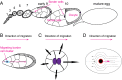
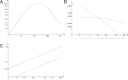
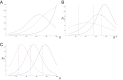
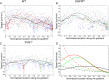
A long-standing question in collective cell migration has been what might be the relative advantage of forming a cluster over migrating individually. Does an increase in the size of a collectively migrating group of cells enable them to sample the chemical gradient over a greater distance because the difference between front and rear of a cluster would be greater than for single cells? We combined theoretical modeling with experiments to study collective migration of the border cells in-between nurse cells in the Drosophila egg chamber. We discovered that cluster size is positively correlated with migration speed, up to a particular point above which speed plummets. This may be due to the effect of viscous drag from surrounding nurse cells together with confinement of all of the cells within a stiff extracellular matrix. The model predicts no relationship between cluster size and velocity for cells moving on a flat surface, in contrast to movement within a 3D environment. Our analyses also suggest that the overall chemoattractant profile in the egg chamber is likely to be exponential, with the highest concentration in the oocyte. These findings provide insights into collective chemotaxis by combining theoretical modeling with experimentation.
Keywords: cell migration; chemotaxis; theoretical modeling; three-dimensional.
Conflict of interest statement
The authors declare no conflict of interest.
Figures


Similar articles
-
Dynamic cluster field modeling of collective chemotaxis.Sci Rep. 2024 Oct 24;14(1):25162. doi: 10.1038/s41598-024-75653-1. Sci Rep. 2024. PMID: 39448677 Free PMC article.
-
Spatial modulation of individual behaviors enables an ordered structure of diverse phenotypes during bacterial group migration.Elife. 2021 Nov 2;10:e67316. doi: 10.7554/eLife.67316. Elife. 2021. PMID: 34726151 Free PMC article.
-
Live Imaging of Border Cell Migration in Drosophila.Methods Mol Biol. 2016;1407:153-68. doi: 10.1007/978-1-4939-3480-5_12. Methods Mol Biol. 2016. PMID: 27271901 Free PMC article.
-
Clustered cell migration: Modeling the model system of Drosophila border cells.Semin Cell Dev Biol. 2020 Apr;100:167-176. doi: 10.1016/j.semcdb.2019.11.010. Epub 2019 Dec 11. Semin Cell Dev Biol. 2020. PMID: 31837934 Review.
-
Long-time viscoelasticity of multicellular surfaces caused by collective cell migration - Multi-scale modeling considerations.Semin Cell Dev Biol. 2019 Sep;93:87-96. doi: 10.1016/j.semcdb.2018.08.002. Epub 2018 Aug 7. Semin Cell Dev Biol. 2019. PMID: 30086376 Review.
Cited by
-
Cell motility in cancer invasion and metastasis: insights from simple model organisms.Nat Rev Cancer. 2018 May;18(5):296-312. doi: 10.1038/nrc.2018.15. Epub 2018 Mar 16. Nat Rev Cancer. 2018. PMID: 29546880 Free PMC article. Review.
-
Collective chemotaxis in a Voronoi model for confluent clusters.Biophys J. 2022 Dec 6;121(23):4624-4634. doi: 10.1016/j.bpj.2022.10.029. Epub 2022 Oct 25. Biophys J. 2022. PMID: 36299235 Free PMC article.
-
Coordination of Receptor Tyrosine Kinase Signaling and Interfacial Tension Dynamics Drives Radial Intercalation and Tube Elongation.Dev Cell. 2018 Apr 9;45(1):67-82.e6. doi: 10.1016/j.devcel.2018.03.011. Dev Cell. 2018. PMID: 29634937 Free PMC article.
-
Dynamical forces drive cell and organ morphology changes during embryonic development.bioRxiv [Preprint]. 2025 Jun 3:2024.07.13.603371. doi: 10.1101/2024.07.13.603371. bioRxiv. 2025. Update in: Proc Natl Acad Sci U S A. 2025 Jul 22;122(29):e2418111122. doi: 10.1073/pnas.2418111122. PMID: 39071435 Free PMC article. Updated. Preprint.
-
Gold Nanorod Photothermal Therapy Alters Cell Junctions and Actin Network in Inhibiting Cancer Cell Collective Migration.ACS Nano. 2018 Sep 25;12(9):9279-9290. doi: 10.1021/acsnano.8b04128. Epub 2018 Aug 27. ACS Nano. 2018. PMID: 30118603 Free PMC article.
References
-
- Parent CA, Devreotes PN. A cell’s sense of direction. Science. 1999;284(5415):765–770. - PubMed
-
- Devreotes PN, Zigmond SH. Chemotaxis in eukaryotic cells: A focus on leukocytes and Dictyostelium. Annu Rev Cell Biol. 1988;4:649–686. - PubMed
-
- Yu SR, et al. Fgf8 morphogen gradient forms by a source-sink mechanism with freely diffusing molecules. Nature. 2009;461(7263):533–536. - PubMed
-
- Crick F. Diffusion in embryogenesis. Nature. 1970;225(5231):420–422. - PubMed
-
- Moissoglu K, Majumdar R, Parent CA. Cell migration: Sinking in a gradient. Curr Biol. 2014;24(1):R23–R25. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Molecular Biology Databases

