Protruding Features of Viral Capsids Are Clustered on Icosahedral Great Circles

Abstract

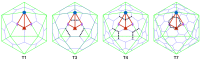
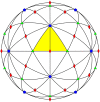
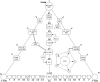
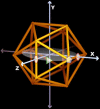
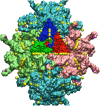
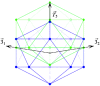
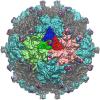
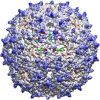
Spherical viruses are remarkably well characterized by the Triangulation (T) number developed by Casper and Klug. The T-number specifies how many viral capsid proteins are required to cover the virus, as well as how they are further subdivided into pentamer and hexamer subunits. The T-number however does not constrain the orientations of these proteins within the subunits or dictate where the proteins should place their protruding features. These protrusions often take the form of loops, spires and helices, and are significant because they aid in stability of the capsid as well as recognition by the host organism. Until now there has be no overall understanding of the placement of protrusions for spherical viruses, other than they have icosahedral symmetry. We constructed a set of gauge points based upon the work affine extensions of Keef and Twarock, which have fixed relative angular locations with which to measure the locations of these features. This work adds a new element to our understanding of the geometric arrangement of spherical viral capsid proteins; chiefly that the locations of protruding features are not found stochastically distributed in an icosahedral manner across the viral surface, but instead these features are found only in specific locations along the 15 icosahedral great circles. We have found that this result holds true as the T number and viral capsids size increases, suggesting an underlying geometric constraint on their locations. This is in spite of the fact that the constraints on the pentamers and hexamer orientations change as a function of T-number, as you need to accommodate more hexamers in the same solid angle between pentamers. The existence of this angular constraint of viral capsids suggests that there is a fitness or energetic benefit to the virus placing its protrusions in this manner. This discovery may have profound impacts on identifying and eliminating viral pathogens, understanding evolutionary constraints as well as bioengineering for capsid drug delivery systems. This result also suggests that in addition to biochemical attachment restrictions, there are additional geometric constraints that should be adhered to when modifying protein capsids.

Fig 1. Triangulation numbers and Constraints.

The standard Triangulation number architecture for spherical capsids ranging from T1 to T7 capsids. Each are composed of 12 pentamers (5-protein units) and a variable number of hexamers (6-protein units). The Asymmetric Unit (AU) for each capsid is shown as a red kite stretching from the 5-fold (blue pentagon) to each of the 2-folds (red diamonds) to the 3-fold axes (green triangle). The icosahedral great circles also encompass each of the 5 distinct red lines shown. As the triangulation number increases, the hexamers must rearrange as seen, which changes the restrictions on their protrusions, shown as dashed lines above. While the capsid proteins are considered to be quasi-equivalent, they are not for the purpose of protrusions. The dotted lines show where modifications for bioengineering will likely be less favorable, except where they intersect with the boundaries of the AU (i.e. the great circles). In general it also appears the p23 within the AU is less favorable. The icosahedral capsids were drawn using the Icosahedral Server [3].

Fig 2. Icosahedral Great Circles.

A view down the 2-fold axes of the 15 icosahedral great circles encompassing the 2-fold (red diamond), 3-fold (green triangle), 5-fold (blue pentagon) symmetry axes, respectively. We found that protruding features cluster on these circles, and are seldom found in the white regions between them, see Fig 3. The spherical area can be subdivided into 60 identical units, known as the Asymmetric Unit (AU), shown here as a yellow (shaded) triangle. Each circle passes through the (5-3-2-3-5-2-5-3-2-3-5-2-5*) fold axes, where 5* indicates the full cycle. The number of intersecting circles determines the symmetry of the point, 2-folds are diamonds, 3-folds are triangles, and 5-folds are pentagons. Additionally that all the gauge points lie on the border of the AU and plane bisecting it and thus are found on the great circles, see Table 1. Note that the full icosahedral group, which includes mirror symmetry, would only required the right hand side of the kite, and would have 120 fundamental domains, also known as the Coxeter Group H3.

Fig 3. Gauge Points.

A schematic of the 21 gauge points within the asymmetric unit which lie between the 2, 3 or 5 fold axes. Gauge points 2 – 14 appear twice as they border the AU, however points 2-6 are equivalent up to a rotation about the 5-fold axes and points 6-14 are equivalent up to a rotation about the 2-fold axes. The angular locations of the gauge points are given in Table 1. The associated gauge points of each virus are indicated as per Table 2. We did not found any viruses with protruding features near gauge points 6-10, 12 and 13.

Fig 4. Asymmetric Unit.

The standard orientation of the icosahedral capsid in the Viper Database [3]. The 2-fold axes are shown as red ovals, the 3-fold axes as green triangles and the 5-folds as blue pentagons. We will use this orientation to measure out spherical angles in Table 1 with ϕ being measured from +z axis towards the x − y plane and θ from the +z axis in the x − z plane. While the asymmetric unit (AU) is not uniquely defined it always contain the volume created by the intersection of three planes containing adjacent icosahedral symmetry vectors, referred to as p52, p53 and p32.

Fig 5. Section of PAV.

A section of the full PAV capsid showing two pentamers (light blue) and two hexameters (pink and green). All 21 gauge points of the AU are displayed as yellow spheres, the 16th gauge point is shown as purple. The 16th gauge point is also known as the local 3-fold, in reference to the AU.

Fig 6. Seneca Valley—is a pseudo T3 virus, with all of its protrusions shown in red.

Some of these protrusions are very minor, being composed of only a few atoms and their results are not reported here. All of the gauge points within the AU are shown in cyan and the gauge point identified with its major protrusion is shown in purple.

Fig 7. Affine Extensions.

We construct the affine extensions of the base icosahedral vertex sets by first translating the polyhedra along one of its symmetry axes, and then applying icosahedral symmetry to the displaced structure. Here we show the base icosahedron (blue) being translated along the 5-fold axes $\left({\overrightarrow{T}}_5\right)$ to form a new icosahedron (green) displaced from the origin. Once icosahedral symmetry about the blue icosahedron is applied, the displaced vertices create new polyhedra at different radii. The displacement lengths are chosen such that at least two of the original vertices intersect the original symmetry axes or intersect neighboring displaced vertices [10]. In this way, we construct a new icosahedral vertex set, adding a radial component to the original icosahedral symmetry. In this example, we intersect the 3-fold axes $\left({\overrightarrow{3}}_{1,2}\right)$ and thus will create a new larger radius dodecahedron. The top vertex of the original icosahedron which now resides at the tip (green) of ${\overrightarrow{T}}_5$ will be the largest radius point, and thus the gauge point of this affine extension.

Fig 8. Pariacoto Virus.

The full PAV (T3) Capsid is made up of 180 identical proteins. It is formed by applying 60 icosahedral rotations of the asymmetric unit (3 proteins in a triangular shape, blue, red and dark green). The blue protein when rotated about the 5-fold axis (gauge point 1) forms a pentamer (5 proteins), of which there are 12 shown in light blue. The red and dark green proteins form pink and green hexamers (6 proteins) when rotated about the 3-fold axes (gauge point 6). The pink and green hexameters meet at a 2-fold axes (gauge point 15). In total there are 20 hexamers, shown in gray. The 16th gauge point, which lies between the 5 and 2 fold axes best describes the outermost features of PAV and is shown as a purple sphere, see Fig 2. showing the alignment of the 16th gauge point (purple sphere) with the outermost features of PAV, which are towers of 3 twisted proteins.

Fig 9. Bacteriophage MS2—is a T3 virus with three surface loops within the AU, however there are 3 additional loops adjacent to the AU on the 5-3 and 2-3 planes.

The capsid is colored radially with the protrusions shown in blue, the nearest gauge points are red spheres with the other gauge points of the AU are shown for reference as green. GA virus is very similar to MS2, and the bottom two loops of GA are lying down near the capsid surface and is not considered as a protrusion, a feature easily noticed using gauge points.

Fig 10. HepB Virus -a T4 virus with many helical bundles, which are perfectly aligned with the gauge points shown as red spheres.

Both strains of HepB share the same protrusions which are the immuno-dominant regions. These protrusions are in excellent agreement with the gauge points. As HepB is eventually enveloped in its lifecycle, the exact spread of the helical bundles are likely important to its lifecycle.

Fig 11. NωV—is a T4 virus with protrusions (purple) that appears to have poor agreement with the gauge point constraints.

The center of mass of its protrusions are far from the gauge points, see Table 2, however the dark blue regions are raised above the average thickness of the capsid and stretch between several gauge points (red spheres), perhaps attempting to conform to the constraints.

Fig 12. HK97 Prohead II—this relatively large T7 virus under goes a maturation to the Head II state, see Fig 13.

Shown here are two of its hexamers (lower half of image) with their protrusions shaded in blue. The most radially distal protrusions are all located near the gauge points, shown in red. Quasiequivalence says the proteins should be nearly identical, however their protrusions are clearly not, as some are recessed into the capsid, seen as lighter blue. This result supports our suggestion of new restrictions for capsid modifications of protrusions.

Fig 13. HK97 Head II—the mature form of HK97 Prohead II.

When the capsid matures, it buckles and the hexamers recede into the capsid leaving the only external feature remaining on its pentamers. This is an example of maturation respecting the constraints of the gauge points.

Fig 14. Simian Virus 40—is an unusual T7 virus that is entirely covered by pentamers instead of the usual hexamers and pentamers.

Shown here are 3 of its pentamers, the upper pentamer is placed in the usual space along the 5-fold axes and is in agreement with the gauge point (red) while the remaining two pentamers are located where you would expect to find hexamers. The protruding features are shown in purple, and while collective their centers of mass are located in the center of the kite sections of the AU region, each protein considered individually (purple) would reduce the angular difference from the gauge points, and are perhaps each in agreement with the gauge points.