Self-Similar Conformations and Dynamics in Entangled Melts and Solutions of Nonconcatenated Ring Polymers
- PMID: 27057066
- PMCID: PMC4819263
- DOI: 10.1021/acs.macromol.5b02319
Self-Similar Conformations and Dynamics in Entangled Melts and Solutions of Nonconcatenated Ring Polymers
Abstract
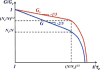
A scaling model of self-similar conformations and dynamics of nonconcatenated entangled ring polymers is developed. Topological constraints force these ring polymers into compact conformations with fractal dimension df = 3 that we call fractal loopy globules (FLGs). This result is based on the conjecture that the overlap parameter of subsections of rings on all length scales is the same and equal to the Kavassalis-Noolandi number OKN ≈ 10-20. The dynamics of entangled rings is self-similar and proceeds as loops of increasing sizes are rearranged progressively at their respective diffusion times. The topological constraints associated with smaller rearranged loops affect the dynamics of larger loops through increasing the effective friction coefficient but have no influence on the entanglement tubes confining larger loops. As a result, the tube diameter defined as the average spacing between relevant topological constraints increases with time t, leading to "tube dilation". Analysis of the primitive paths in molecular dynamics simulations suggests a complete tube dilation with the tube diameter on the order of the time-dependent characteristic loop size. A characteristic loop at time t is defined as a ring section that has diffused a distance equal to its size during time t. We derive dynamic scaling exponents in terms of fractal dimensions of an entangled ring and the underlying primitive path and a parameter characterizing the extent of tube dilation. The results reproduce the predictions of different dynamic models of a single nonconcatenated entangled ring. We demonstrate that traditional generalization of single-ring models to multi-ring dynamics is not self-consistent and develop a FLG model with self-consistent multi-ring dynamics and complete tube dilation. This selfconsistent FLG model predicts that the longest relaxation time of nonconcatenated entangled ring polymers scales with their degree of polymerization N as τrelax ~ N7/3, while the diffusion coefficient of these rings scales as D3d ~ N-5/3. For the entangled solutions and melts of rings, we predict power law stress relaxation function G(t) ~ t-3/7 at t < τrelax without a rubbery plateau and the corresponding viscosity scaling with the degree of polymerization N as η ~ N4/3. These theoretical predictions are in good agreement with recent computer simulations and are consistent with experiments of melts of nonconcatenated entangled rings.
Conflict of interest statement
The authors declare no competing financial interest.
Figures
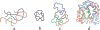
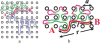
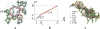


References
-
- Rubinstein M, Colby RH. Polymer Physics. OUP; Oxford: 2003.
-
- Kavassalis TA, Noolandi J. Phys Rev Lett. 1987;59:2674–2677. - PubMed
-
- Kavassalis TA, Noolandi J. Macromolecules. 1988;21:2869–2879.
-
- Kavassalis TA, Noolandi J. Macromolecules. 1989;22:2709–2720.
-
- Doi M, Edwards SF. The Theory of Polymer Dynamics. Clarendon Press; Oxford: 1986.
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials
Miscellaneous
